Understanding Alternate Exterior Angles
Table of Contents
Introduction
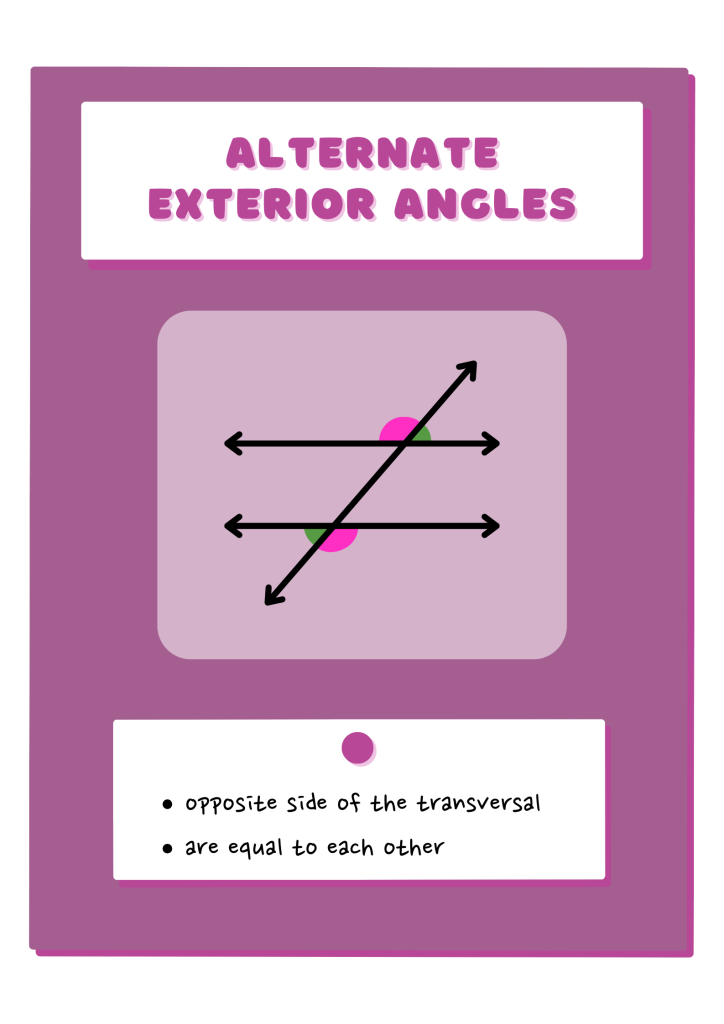
Alternate Exterior Angles
Alternate exterior angles are a fundamental concept in geometry that arises when dealing with intersecting lines and transversals. Let’s delve into the realm of alternate exterior angles and explore their significance in geometric relationships.
Analogy of Definition
What are Alternate Exterior Angles?
Alternate exterior angles refer to a pair of angles that are formed on the exterior side of two lines when intersected by a transversal. These angles are positioned on opposite sides of the transversal and have specific geometric properties.
Alternate exterior angles are like the cool cousins of alternate interior angles. They hang out on the outside of parallel lines when a third line (called a transversal) crosses through them.
Imagine you have two parallel lines and a third line cutting across them. Look at the angles formed on the outside of the parallel lines, but on opposite sides of the transversal. These are your alternate exterior angles.
Just like alternate interior angles, alternate exterior angles also have a special bond: they are always equal. So if you measure one of them, you’ll find that the other one has the same measurement. It’s like they’re mirror images of each other, reflecting the same angle measure.
Understanding alternate exterior angles is super helpful because they pop up in all sorts of geometry problems, helping us solve puzzles about angles and lines.
Method
Identifying Alternate Exterior Angles
To identify alternate exterior angles, locate the angles that are positioned outside the intersected lines and are situated on opposite sides of the transversal. Understanding the properties of parallel lines and transversals is essential in recognizing alternate exterior angles.
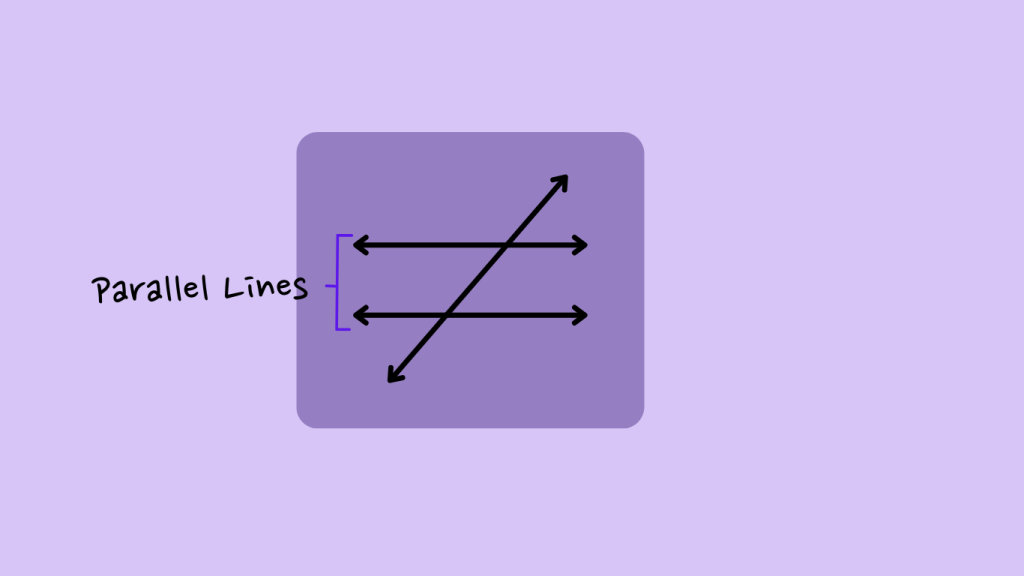
Find Parallel Lines: First, locate two lines that are parallel to each other. Picture them like railroad tracks, running side by side without ever touching.
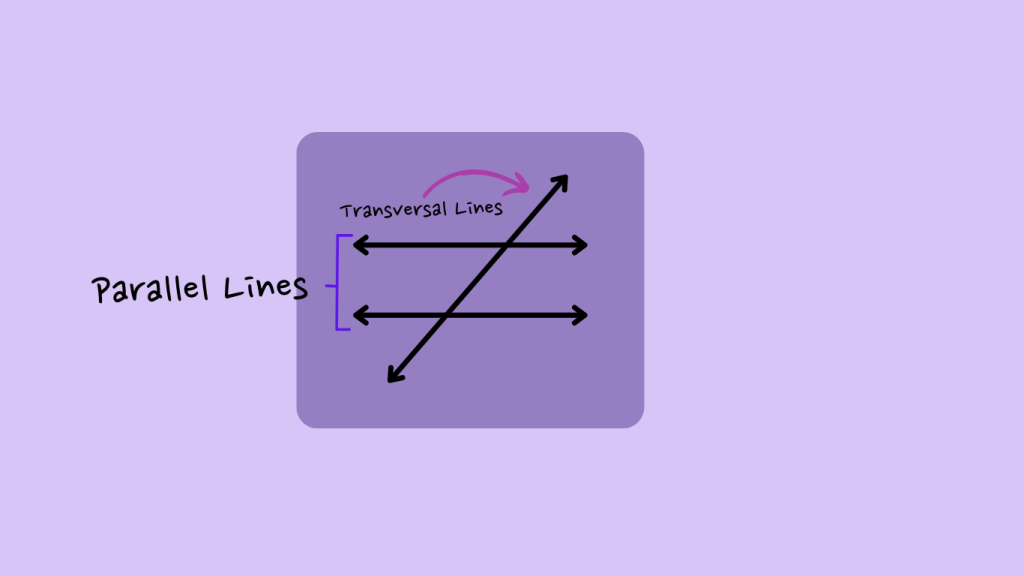
Spot the Transversal: Next, look for another line (the transversal) that cuts through those parallel lines. It’s like a road crossing over the railroad tracks.
Look Outside the Parallel Lines: Now, focus on the angles formed outside the parallel lines, but on opposite sides of the transversal. These are your alternate exterior angles.
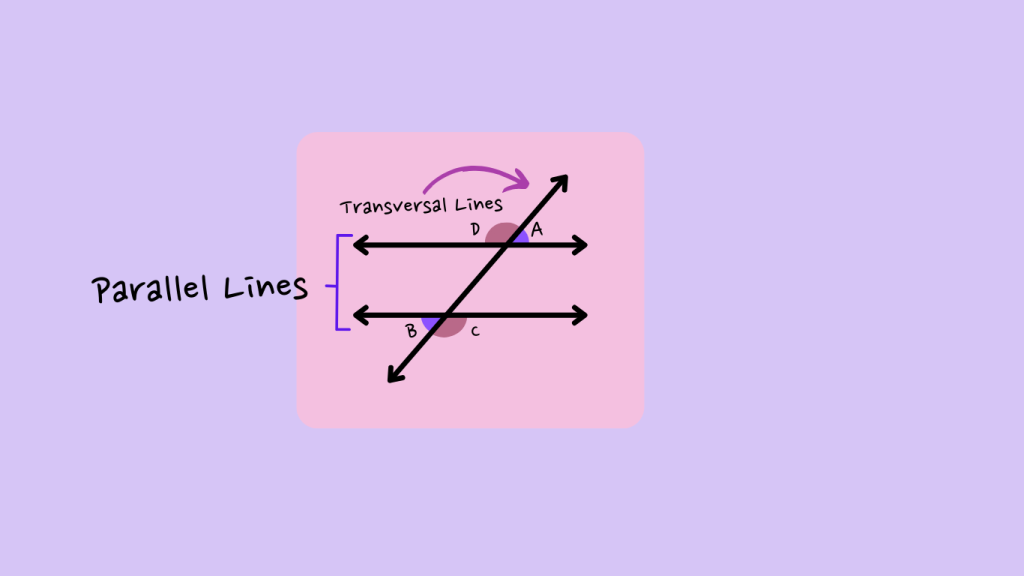
Check for Equality: Remember, alternate exterior angles are always equal. So if you measure one angle and find its value, you’ll see that the other alternate exterior angle has the same measurement.
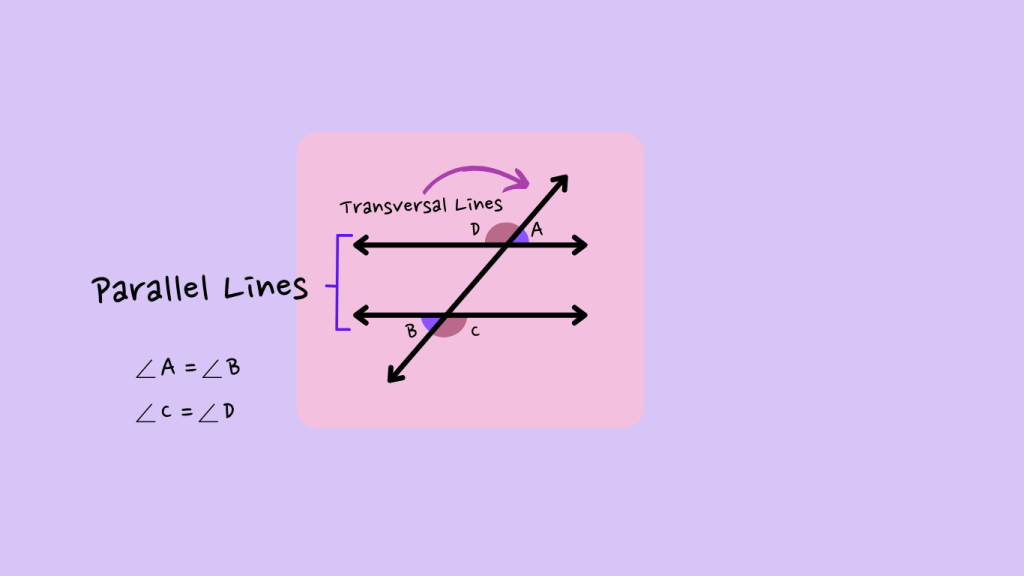
Just like with alternate interior angles, spotting alternate exterior angles helps us unlock solutions to geometry problems and understand how lines intersect in different ways.
Examples
Example 1: Identify the alternate exterior angles, and find e.
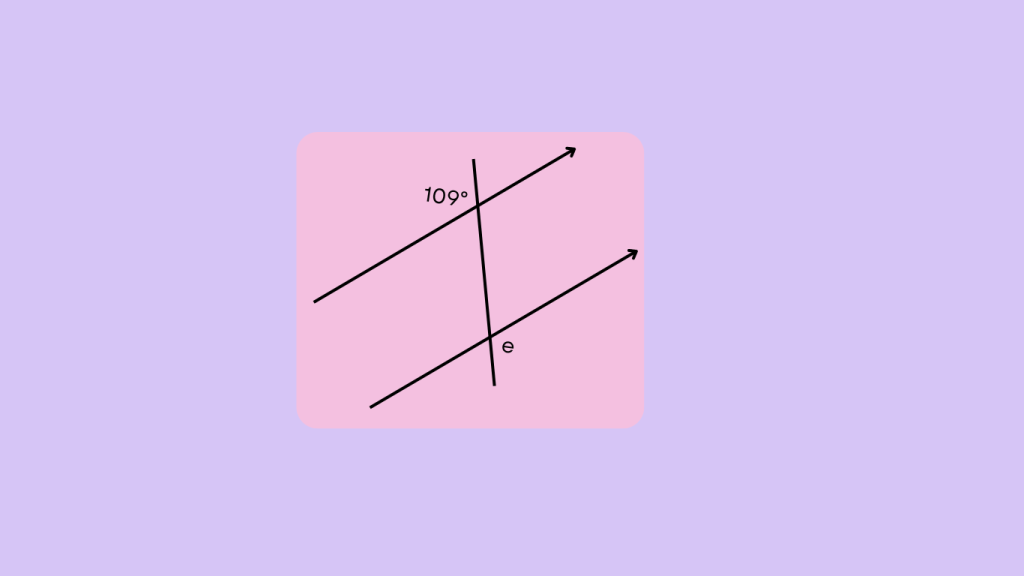
We know,
The alternate exterior angle of is ∠e is 105°, so ∠e is 105°.
Example 2: In the figure below, lines l and m are parallel, and transversal t intersects them. Identify the alternate exterior angles, and find x.
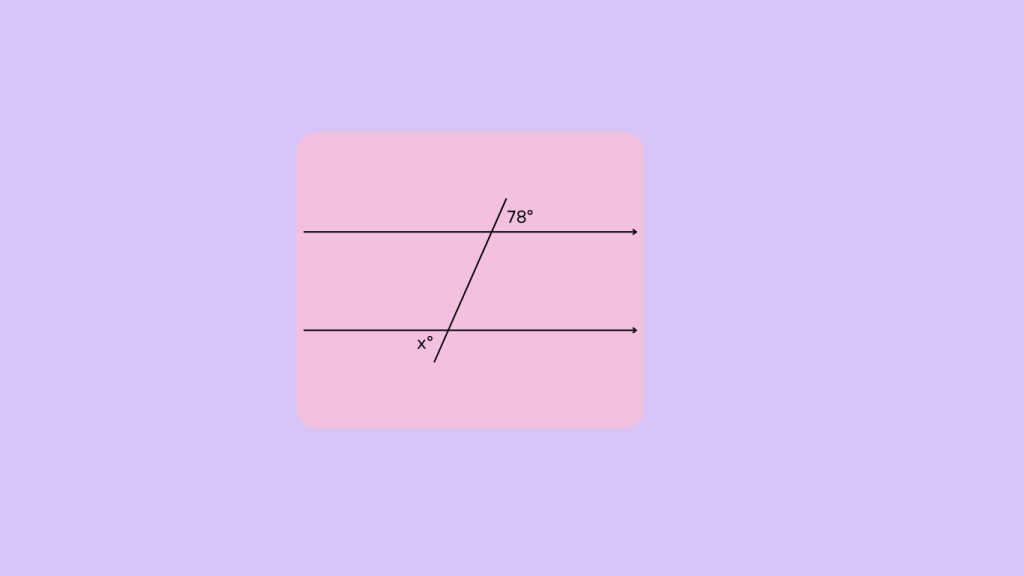
We know,
The alternate exterior angle of is ∠x is 78°, so ∠x is 78°.
Summary:
This example illustrates the concept of alternate exterior angles in a scenario involving parallel lines and a transversal. By identifying the angles located on the exterior side of the lines and positioned on opposite sides of the transversal, the alternate exterior angles are determined, showcasing their significance in geometric relationships.
This example illustrates the concept of alternate exterior angles in a scenario involving parallel lines and a transversal. By identifying the angles located on the exterior side of the lines and positioned on opposite sides of the transversal, the alternate exterior angles are determined, showcasing their significance in geometric relationships.
Quiz
Tips and Tricks
1. Angle Relationships
Tip: Look for the angles located outside the intersected lines and positioned on opposite sides of the transversal to identify alternate exterior angles.
2. Parallel Lines
Tip: Recognize the relationship between parallel lines and transversals to comprehend the concept of alternate exterior angles.
3. Real-Life Applications
Tip: Explore real-life scenarios where parallel lines and transversals are encountered, showcasing the practical significance of alternate exterior angles.
Real life application
Scenario: Architectural Design
In architectural design, the concept of alternate exterior angles is utilized in creating structures with parallel lines and transversals, ensuring the proper alignment and symmetry of architectural elements.
Scenario: Engineering Blueprint
Engineers apply the concept of alternate exterior angles in blueprint designs, where parallel lines and transversals play a crucial role in the layout and construction of various structures.
Scenario: Interior Design
Interior designers use the understanding of alternate exterior angles to create visually appealing spaces by incorporating parallel lines and transversals in the design layout.
FAQ's
Alternate exterior angles are a pair of angles that are formed when a transversal intersects two lines. They are located on the exterior side of the two lines and are positioned on opposite sides of the transversal.
Alternate exterior angles are congruent, meaning they have the same measure. When the lines intersected by the transversal are parallel, the alternate exterior angles are equal in measure.
Understanding alternate exterior angles is crucial in geometry as it helps in solving problems related to parallel lines and transversals. It also plays a key role in proving theorems and properties of angles.
Yes, the concept of alternate exterior angles can be applied in real-life scenarios such as architecture, engineering, and design, where parallel lines and transversals are encountered.
To identify alternate exterior angles, look for the angles that are located outside the two intersected lines and are positioned on opposite sides of the transversal.
Like? Share it with your friends
Facebook
Twitter
LinkedIn