Understanding Complementary Angles
Table of Contents
Introduction
Complementary Angles
In the realm of geometry, the concept of complementary angles holds significant importance. Let’s delve into the world of angles and explore the definition and significance of complementary angles in various contexts.
Analogy of Definition
What are Complementary Angles?
Complementary angles refer to a pair of angles whose sum equals 90 degrees. When combined, they form a right angle, making them an essential element in understanding geometric relationships and measurements.
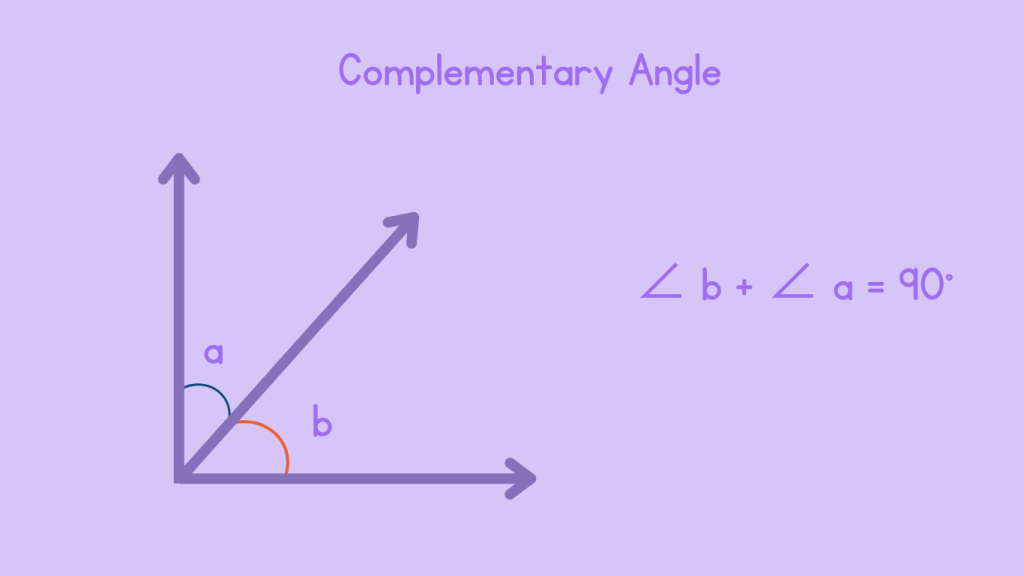
Method
Types of Complementary Angles
Complementary angles are two angles whose measures add up to 90 degrees. They are essential in various geometric and trigonometric applications. Understanding the different types of complementary angles can help in solving geometric problems and recognizing angle relationships in various contexts. Here are the primary types of complementary angles:
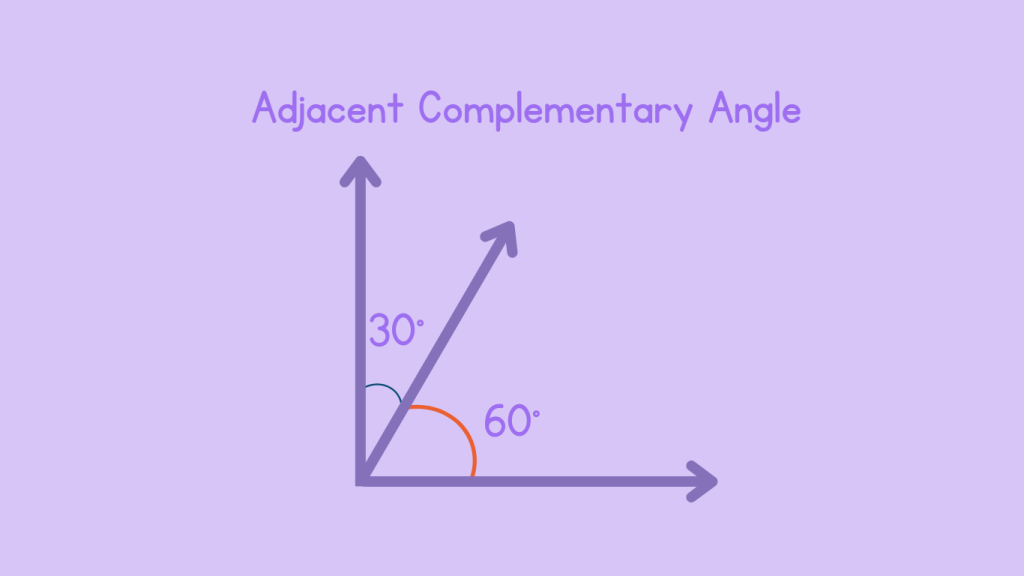
1. Adjacent Complementary Angles
Adjacent complementary angles share a common vertex and a common side, lying next to each other. When placed adjacent to each other, they form a right angle. For example, if angle A measures 30 degrees and angle B measures 60 degrees, and they share a common side, they are adjacent complementary angles.
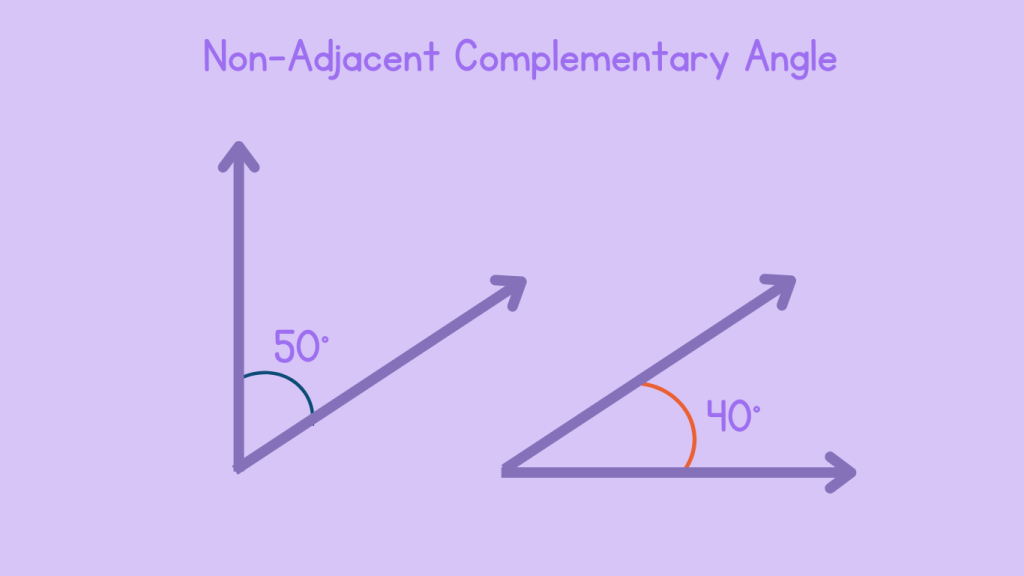
2. Non-Adjacent Complementary Angles
Non-adjacent complementary angles do not share a common vertex or side. They are separate from each other but their measures still sum to 90 degrees. These angles can be located anywhere in a plane. For instance, if angle C measures 45 degrees and angle D measures 45 degrees, they are non-adjacent complementary angles.
Examples
Summary:
This example illustrates the concept of complementary angles, where Angle 1 and Angle 2, with measures of 30 degrees and 60 degrees respectively, add up to 90 degrees, forming a right angle. This demonstrates the fundamental property of complementary angles in geometry.
This example illustrates the concept of complementary angles, where Angle 1 and Angle 2, with measures of 30 degrees and 60 degrees respectively, add up to 90 degrees, forming a right angle. This demonstrates the fundamental property of complementary angles in geometry.
Quiz
Tips and Tricks
1. Remember the Definition
Tip:Complementary angles always sum up to 90 degrees. This is the most fundamental aspect to keep in mind.
2. Quick Calculation
Tip:If you know one angle, subtract it from 90 degrees to find its complement. For example, if one angle is 30 degrees, the complementary angle is 90 – 30 = 60 degrees.
3. Common Angle Pairs
Tip:Familiarize yourself with common complementary pairs: 30 degrees and 60 degrees, 45 degrees and 45 degrees, 20 degrees and 70 degrees, 15 degrees and 75 degrees
4. Right-Angle Relationships
Tip:Complementary angles often appear in right triangles, where the two non-right angles are complementary. This helps in solving problems involving right triangles.
Real life application
Scenario: The Architect’s Blueprint
An architect utilizes the concept of complementary angles when designing structures to ensure precise angles and measurements for stability and aesthetics. By understanding complementary angles, the architect can create visually appealing and structurally sound buildings.
Scenario: Navigating at Sea
Mariners rely on the knowledge of complementary angles to navigate at sea, using the angles formed by celestial bodies to determine their position and course. Understanding complementary angles is essential for accurate navigation and safe voyages.
FAQ's
Complementary angles are two angles whose sum is 90 degrees. When added together, they form a right angle.
Complementary angles add up to 90 degrees, while supplementary angles add up to 180 degrees. Complementary angles form a right angle, whereas supplementary angles form a straight line.
Yes, complementary angles can be adjacent, meaning they share a common vertex and side while not overlapping.
Complementary angles are directly related to right angles, as their sum equals 90 degrees, which is the measure of a right angle.
Complementary angles find practical applications in various real-life situations, such as in carpentry, architecture, and navigation, where understanding angles is crucial for accurate measurements and designs.
Like? Share it with your friends
Facebook
Twitter
LinkedIn