Understanding Corresponding Angles
Table of Contents
Introduction
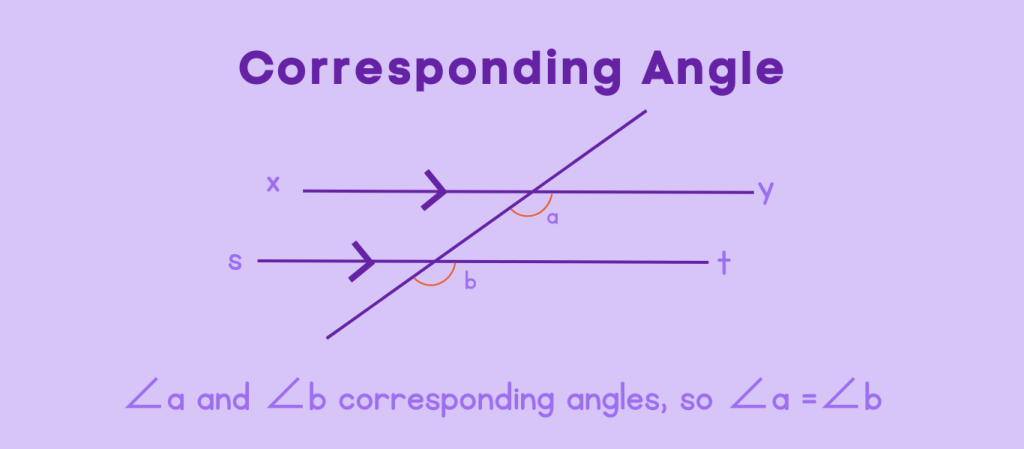
Corresponding Angles
In the realm of geometry, the concept of corresponding angles plays a very pivotal role in understanding the relationships between intersecting lines and the measures of angles formed. Let’s delve into the world of corresponding angles and unravel their significance in geometric contexts.
Analogy of Definition
What are Corresponding Angles?
Corresponding angles are a fundamental concept in geometry, particularly in the study of parallel lines cut by a transversal. These angles have specific properties that define their relationship and make them a valuable tool for solving geometric problems. Mathematically, we can define corresponding angles as follows:
A pair of angles formed by two parallel lines and a transversal are considered corresponding angles if and only if:
- One angle is located in the interior region between the parallel lines, while the other is located in the exterior region outside the parallel lines.
- Both angles lie on the same side of the transversal.
- The angles do not share the same vertex.
These properties help to identify and distinguish corresponding angles in various geometric configurations.
Method
Identifying Corresponding Angles
Identifying corresponding angles in geometric figures is a critical skill, especially when working with parallel lines and a transversal. Corresponding angles are pairs of angles that have specific properties which distinguish them from other types of angles. Here’s a step-by-step guide to help you identify corresponding angles effectively:
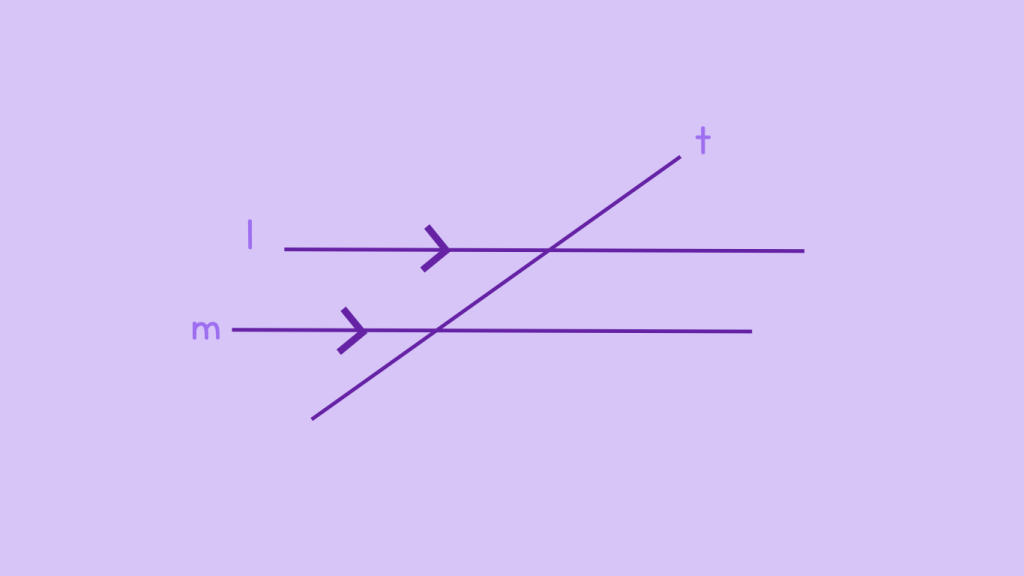
Step 1: Identify the Parallel Lines and Transversal
Let’s say line l and line m are parallel, and line t is the transversal.
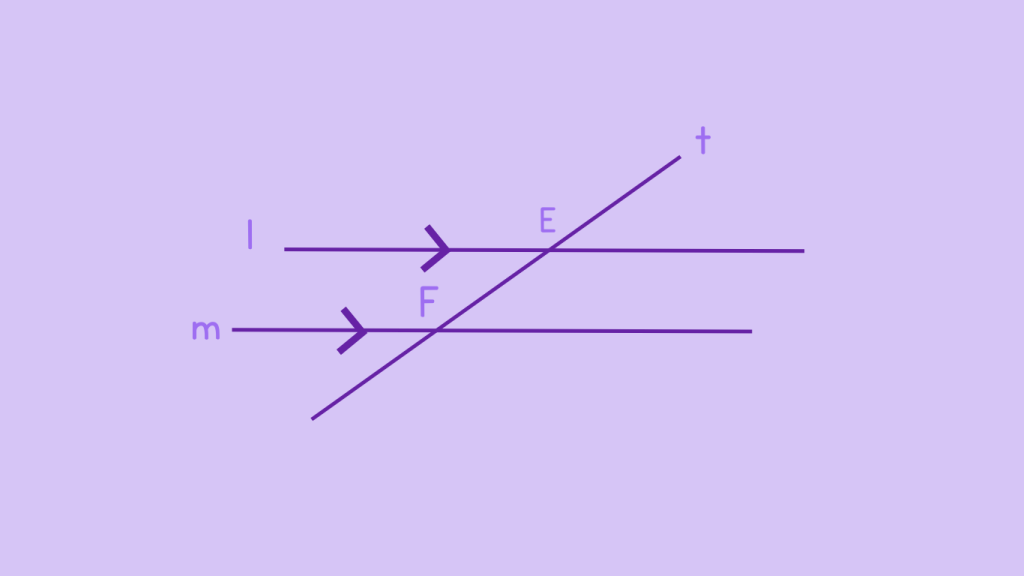
Step 2: Locate Intersection Points
The transversal t intersects line l at point E and line m at point F
.
Step 3: Identify Angles
At point A, you have four angles: ∠a,∠b ∠,c,∠d
At point B, you have four angles: ∠w,∠x,∠y ,∠z
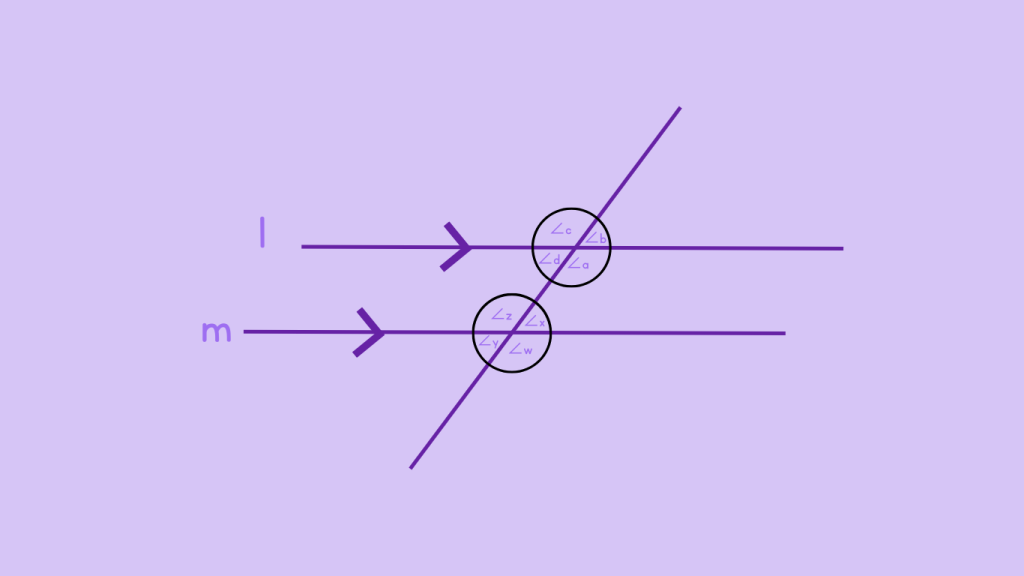
Step 4: Match Interior and Exterior Angles
Suppose,
∠a is in the interior region and ∠w is its corresponding angle in the exterior region.
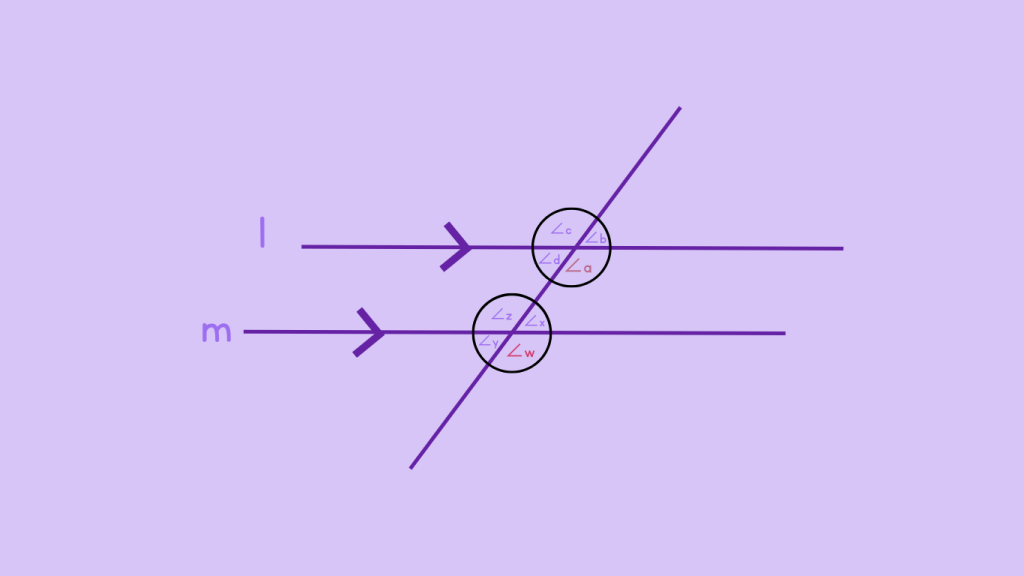
Step 5: Check Same Side of Transversal
If ∠a and ∠w are both on the left side of the transversal, then they are corresponding angles.
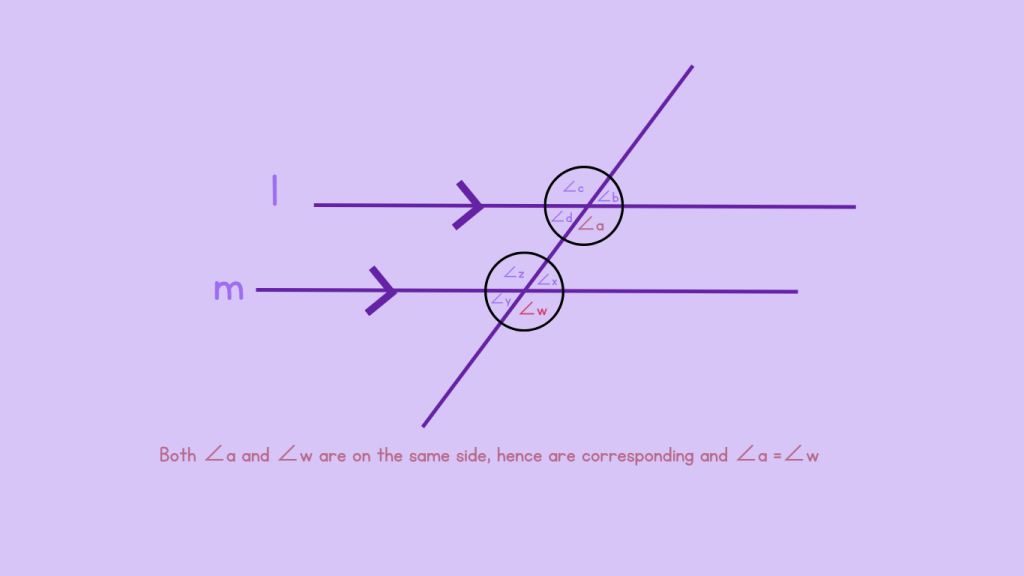
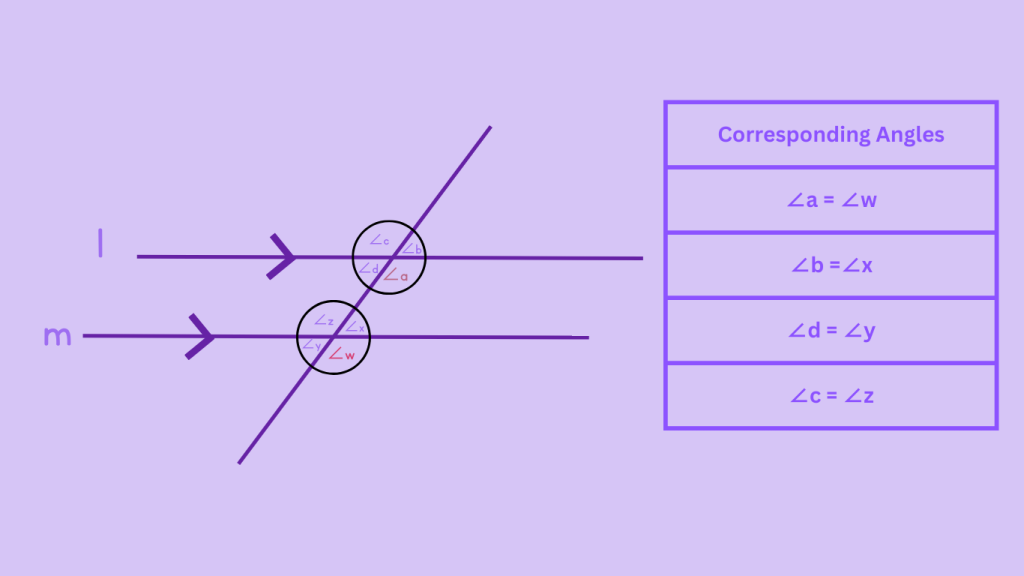
By following these steps, you can accurately identify pairs of corresponding angles in various geometric figures. This methodical approach ensures you understand their placement and properties, which is essential for solving geometric problems and proving relationships within figures. In the figure above the following are the pairs of corresponding angles:
Examples
Example 1: Find the value of x
Quiz
Tips and Tricks
1. Identifying Corresponding Angles
Tip: Look for angles that are in the same position at each intersection and have equal measures.
2. Solving Geometric Problems
Tip: Utilize the congruence of corresponding angles to determine unknown angle measures and establish parallelism of lines.
3. Real-Life Applications
Tip: Observe the angles formed by intersecting lines to analyze their relationships and congruence.
Real life application
Scenario 1: Architectural Designs
In architectural designs, corresponding angles are utilized to ensure the symmetry and balance of structures, especially in the construction of buildings, bridges, and geometric patterns.
Scenario 2: Road Intersections
Corresponding angles play a crucial role in road intersections, where the angles formed by intersecting roads and traffic signals are analyzed to ensure safe and efficient traffic flow.
Scenario 3: Geometric Patterns
Geometric patterns often incorporate corresponding angles to create visually appealing designs and symmetrical arrangements.
FAQ's
Corresponding angles are pairs of angles that are formed when a transversal intersects two lines. They are located in the same position at each intersection and also have equal measures.
Corresponding angles are related to parallel lines as they are congruent when the lines are parallel. This means that their measures are equal, and they have the same degree of rotation.
Yes, corresponding angles can be found in various real-life situations such as architectural designs, road intersections, and geometric patterns.
Understanding corresponding angles is crucial in geometry as it helps in identifying congruent angles, solving geometric problems, and analyzing the relationships between intersecting lines.
Corresponding angles can be utilized to determine the measures of unknown angles, prove the congruence of angles, and establish the parallelism of lines in geometric problem-solving.
Like? Share it with your friends
Facebook
Twitter
LinkedIn