Understanding Obtuse Angles – Definition and Properties
Table of Contents
Introduction
Obtuse Angles
In the realm of geometry, the concept of Obtuse Angles plays a significant role in defining spatial relationships and geometric properties. Let’s delve into the world of Obtuse Angles and explore their definition, properties, types, and practical applications.
Analogy of Definition
What are Obtuse Angles?
An Obtuse Angle is a speacific type of angle that measures greater than 90 degrees (right angle) but less than 180 degrees(straight angle).
Obtuse angles are a bit like the cool kids of the geometry world. They’re not your average, run-of-the-mill angles – they’re special. An obtuse angle is an angle that is greater than 90 degrees but less than 180 degrees.
Imagine you have a straight line, and you bend it a bit, but not too much – just enough so that it’s bigger than a right angle (which is exactly 90 degrees). That bend you’ve made? That’s an obtuse angle.
You can think of obtuse angles as those angles that are “wide open.” They’re not all cramped up like acute angles (which are smaller than 90 degrees), nor are they straight like right angles. They’re somewhere in between – a bit stretched out and spacious.
Method
Identifying Obtuse Angles
To identify an Obtuse Angle, measure the angle using a protractor. If the angle measures greater than 90 degrees but less than 180 degrees, it is classified as an Obtuse Angle.
Let’s identify whether the following angle is obtuse or not using a protractor.
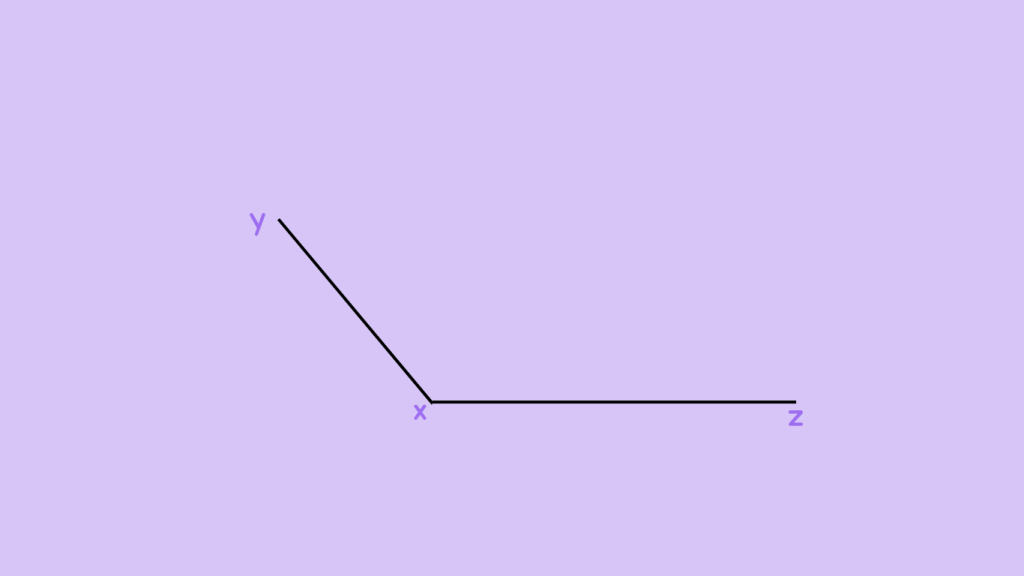
Place the Protractor: First, align the bottom edge of the protractor with one side of the angle. Make sure the center point of the protractor is positioned at the vertex (the point where the two lines meet), which is ‘x’ in this.
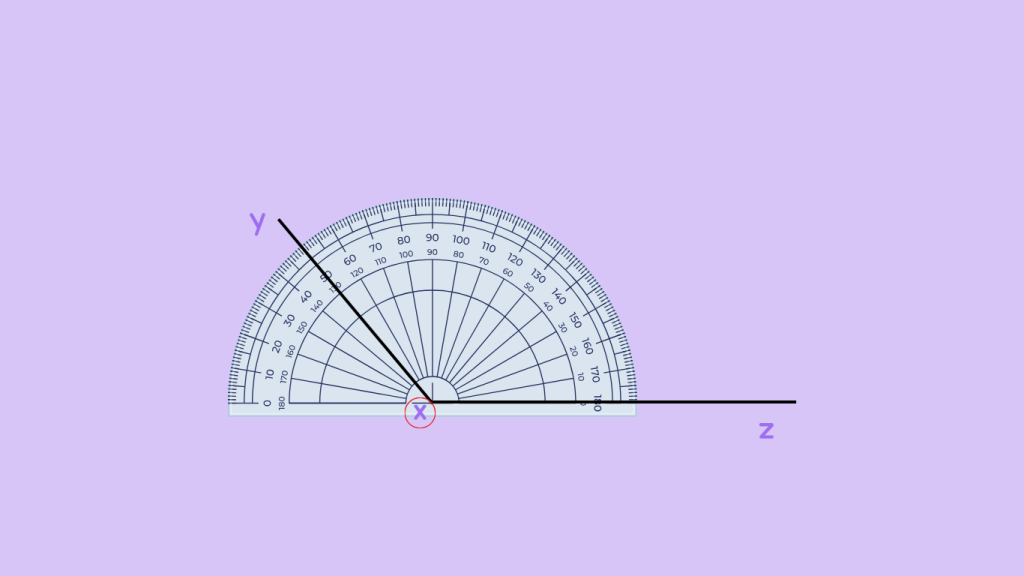
Read the Scale: Look at the scale of the protractor. It typically ranges from 0 degrees to 180 degrees, with 90 degrees marked as a right angle.
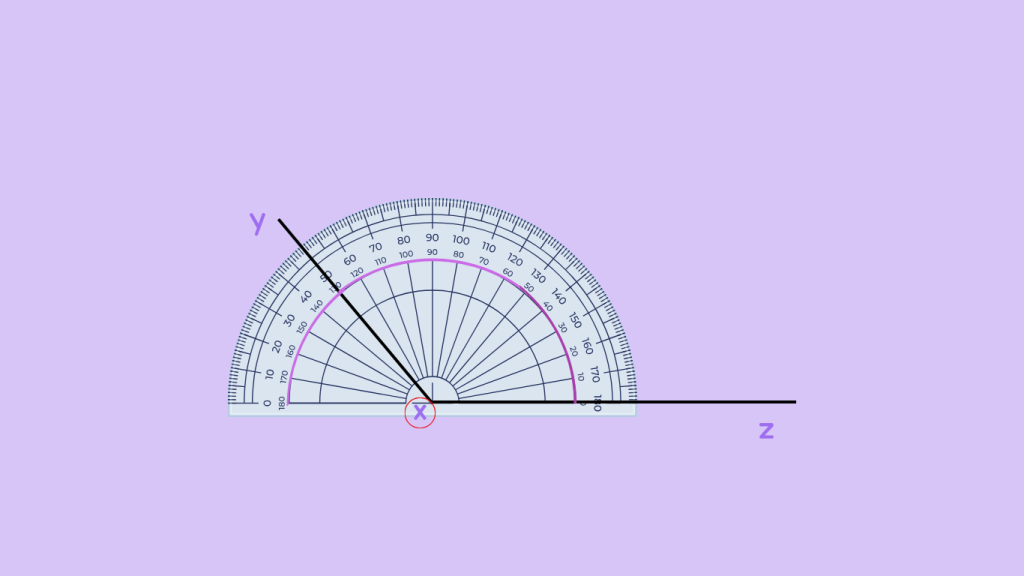
Measure the Angle: Determine the measurement of the angle by reading the degree markings where the other side of the angle intersects the scale. If the measurement falls between 90 degrees and 180 degrees, it’s an obtuse angle.
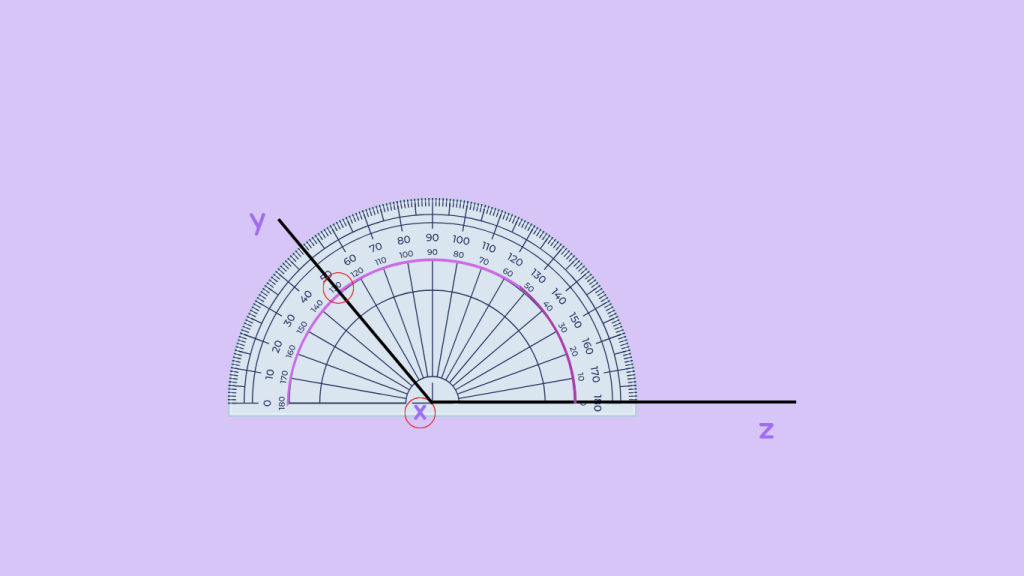
Verify the Angle: Double-check your measurement to ensure accuracy. If the angle is greater than 90 degrees but less than 180 degrees, it qualifies as an obtuse angle.
Remember, obtuse angles are wider than right angles (90 degrees) but less than straight angles (180 degrees). So, if the angle you measured opens up more than a right angle but less than a straight angle, you’ve identified an obtuse angle!
Understanding the properties of obtuse angles not only helps in identifying and classifying them but also aids in solving geometric problems and analyzing structures. In this article, we’ll explore the defining features and properties of obtuse angles, providing insights into their nature and significance.
Properties of Obtuse Angles
- An obtuse angle measures greater than 90 degrees but less than 180 degrees.
- It is wider than a right angle (90 degrees).
- The arms of an obtuse angle extend in opposite directions from the vertex.
- The exterior sides of an obtuse angle form a straight line with an interior angle.
- In a triangle, if one angle is obtuse, the sum of the other two angles is less than 90 degrees (acute).
- In a quadrilateral, at least one angle must be obtuse if the sum of the other three angles is less than 360 degrees.
- An obtuse angle can be bisected to form two acute angles.
- The complement of an obtuse angle is always acute.
In real-world scenarios, obtuse angles are commonly found in structures such as rooflines, mountain slopes, and road intersections.
These properties provide a comprehensive understanding of obtuse angles, facilitating their identification, analysis, and application in geometry and beyond.
Examples
Few examples of Obtuse Angles
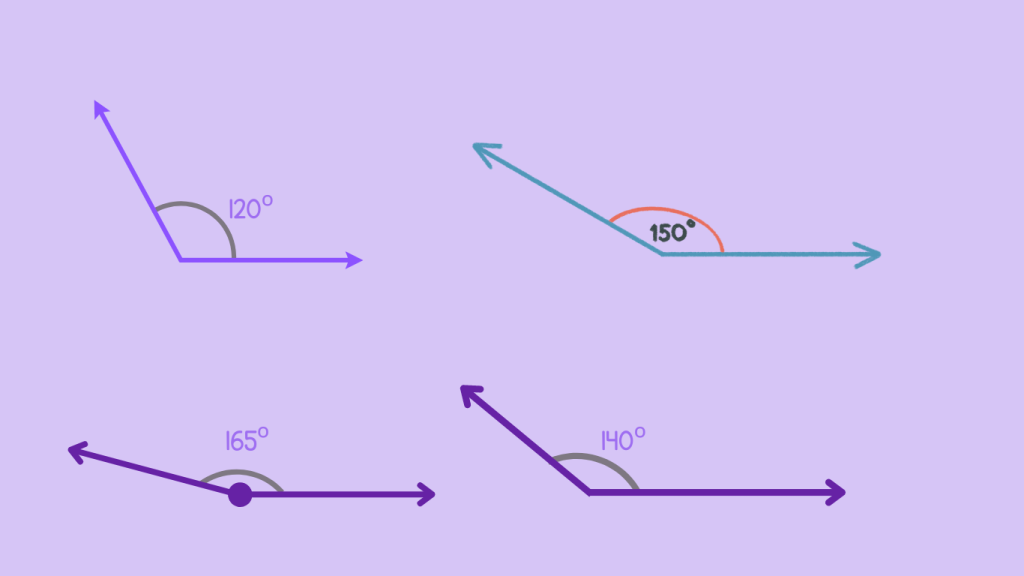
These examples illustrate the process of identifying Obtuse Angles by measuring the angle using a protractor. If the measurement falls within the range of 90 to 180 degrees, the angle is classified as an Obtuse Angle. This understanding is essential in geometry and spatial reasoning, enabling individuals to recognize and work with Obtuse Angles effectively.
Quiz
Tips and Tricks
1. Visualize with Everyday Objects
Tip: Use everyday objects like a door hinge or the hands of a clock to visualize obtuse angles. For example, when a door is open more than halfway, the angle between the door and the door frame is obtuse.
2. Compare with Right and Straight Angles
Tip: Remember that obtuse angles are wider than right angles (90 degrees) but narrower than straight angles (180 degrees). Visualizing these comparisons can help identify obtuse angles more easily.
3. Look for Diagonals
Tip: In polygons, look for diagonals connecting non-adjacent vertices. If the angle formed by the intersection of these diagonals is greater than 90 degrees but less than 180 degrees, it’s an obtuse angle.
4. Bisect to Find Acute Angles
Tip: If you have an obtuse angle and need to find acute angles, bisect the obtuse angle using a straightedge. This will divide the obtuse angle into two smaller acute angles.
5. Use a Protractor
Tip: When measuring angles with a protractor, remember that obtuse angles will have their measurements fall between 90 and 180 degrees. Align the protractor carefully to accurately measure obtuse angles.
Real life application
Real-Life Applications of Obtuse Angles:,
Story: The Architect’s Challenge
An architect was tasked with designing a modern building featuring unique geometric elements. The architect utilized the concept of Obtuse Angles to create innovative structural designs and captivating architectural features.
Challenge 1: The Rooftop Oasis
The architect envisioned a rooftop garden with a glass canopy, requiring the incorporation of Obtuse Angles in the design to achieve the desired aesthetic and structural stability.
Challenge 2: The Grand Atrium
The central atrium of the building was designed with soaring ceilings and expansive windows, showcasing the elegance of Obtuse Angles in creating a sense of openness and grandeur.
Challenge 3: The Geometric Facade
The building’s facade featured geometric patterns and angular elements, with Obtuse Angles serving as the foundation for the captivating visual appeal and modern architectural expression.
FAQ's
Like? Share it with your friends
