Understanding the Scalene Triangle – Definition and Examples
Table of Contents
Introduction
Scalene Triangle
In the realm of geometry, the concept of a scalene triangle holds significance due to its unique properties and applications. Let’s delve into the world of scalene triangles to gain a comprehensive understanding of their definition, properties, and real-life examples.
Analogy of Definition
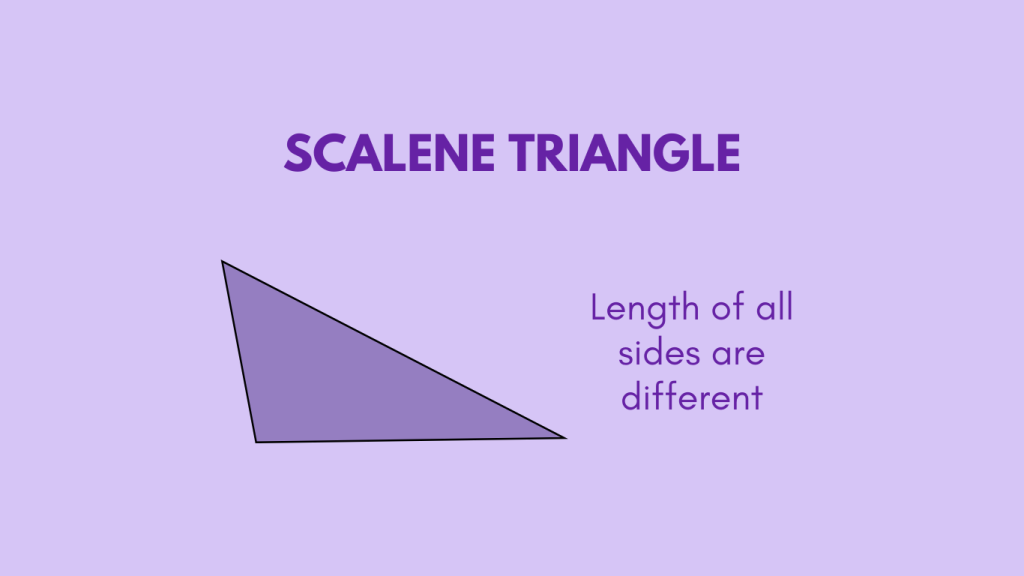
What is a Scalene Triangle?
A scalene triangle is a geometric figure characterized by having three unequal sides and three unequal angles. This distinct feature sets it apart from other types of triangles, making it an essential concept in geometry.
Method
Properties of a Scalene Triangle
A scalene triangle is a type of triangle in which all three sides have different lengths. Unlike isosceles or equilateral triangles, which have at least two sides of equal length, a scalene triangle exhibits no symmetry in terms of side lengths. This unique characteristic gives rise to several properties that distinguish scalene triangles from other types of triangles:
Unequal Side Lengths: The most defining property of a scalene triangle is that all three sides have different lengths. This means that no two sides are equal in length, leading to a lack of symmetry in the triangle’s shape.
Unequal Angles: Due to the varying side lengths, the angles of a scalene triangle are also unequal. Each angle corresponds to the length of the side opposite it, leading to a diverse range of angle measures within the triangle.
Angle Sum Property: Like all triangles, the sum of the interior angles of a scalene triangle is always 180 degrees. However, unlike equilateral or isosceles triangles, where some angles are congruent, the angles of a scalene triangle are all distinct, contributing to the variability in angle measures.
No Symmetry: Unlike isosceles or equilateral triangles, which exhibit some form of symmetry, scalene triangles lack any inherent symmetry due to their unequal side lengths and angles. This property makes scalene triangles versatile and applicable in a wide range of geometric contexts.
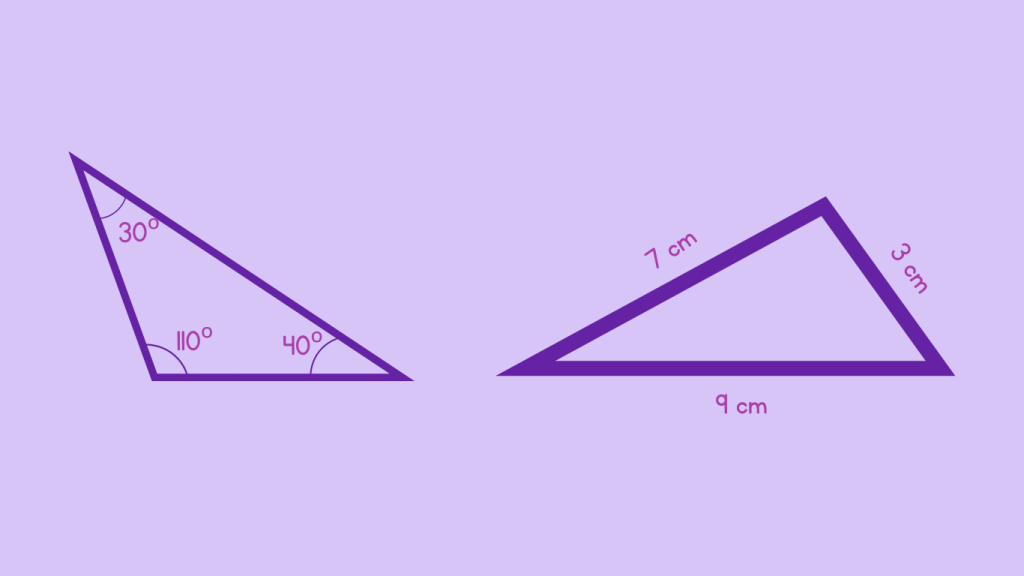
Examples
Summary: This example illustrates the properties of a scalene triangle, showcasing the inequality of side lengths and interior angles, as well as the absence of symmetry lines. Additionally, it emphasizes the fundamental property that the sum of any two sides of a scalene triangle always exceeds the length of the third side, reinforcing its unique characteristics.
Quiz
Tips and Tricks
1. Identifying Scalene Triangles
Tip: To identify a scalene triangle, compare the side lengths and angles to determine inequality.
2. Perimeter of Scalene Triangle
Tip: Perimeter Calculation: To find the perimeter of a scalene triangle, simply add the lengths of all three sides together. Since the sides are different lengths, make sure to add them accurately to obtain the total perimeter.
3. Pythagorean Theorem
Tip: In some cases, the Pythagorean Theorem can be applied to scalene triangles to find the length of one side if the lengths of the other two sides are known and the triangle is a right triangle.
4. Area of Scalene Triangle
Tip: You can use the base and height method if you know the length of one side and the perpendicular distance from the opposite vertex to that side. The formula to find out area is \frac{1}{2} × base ×height, or you can also use heron’s formula.
Real life application
Story: The Architect’s Challenge
An architect faced a challenge in designing a unique roof structure for a modern building. To achieve the desired aesthetic, the architect utilized the concept of scalene triangles to create an innovative and visually striking roof design, showcasing the practical application of scalene triangles in architecture.
Challenge 1: The Musical Instrument Design
A luthier sought to craft a new musical instrument with a distinctive shape and sound. By incorporating the principles of scalene triangles into the instrument’s design, the luthier achieved a harmonious blend of aesthetics and acoustics, exemplifying the real-life application of scalene triangles in the creation of musical instruments.
FAQ's
A scalene triangle is a type of triangle that has three unequal sides and three unequal angles. In other words, no two sides or angles are the same in a scalene triangle.
The properties of a scalene triangle include unequal side lengths, unequal interior angles, and no lines of symmetry. Additionally, the sum of any two sides of a scalene triangle is always greater than the length of the third side.
Yes, a scalene triangle can have a right angle, but it can also have acute or obtuse angles. The key characteristic of a scalene triangle is the inequality of its sides and angles.
A scalene triangle differs from an equilateral triangle in that all three sides of an equilateral triangle are equal in length, while the sides of a scalene triangle are all different lengths.
Real-life examples of scalene triangles can be found in various architectural structures, such as the Eiffel Tower, as well as in the design of musical instruments like violins and guitars.
Like? Share it with your friends
Facebook
Twitter
LinkedIn