Understanding the Centroid of a Triangle
Table of Contents
Introduction
Centroid of a Triangle
The Centroid of a Triangle is a fundamental concept in geometry, representing the point of intersection of the medians of a triangle. Let’s delve into the definition, formula, and properties of the Centroid of a Triangle to gain a comprehensive understanding of its significance in geometric calculations and constructions.
Analogy of Definition
What is the Centroid of a Triangle?
The Centroid of a Triangle is the point of concurrency of the medians, which are the line segments joining each vertex to the midpoint of the opposite side. In the triangle ABC, point Z is the centroild. The centroid intersects the medians of the triangle in a 2:1 ratio.
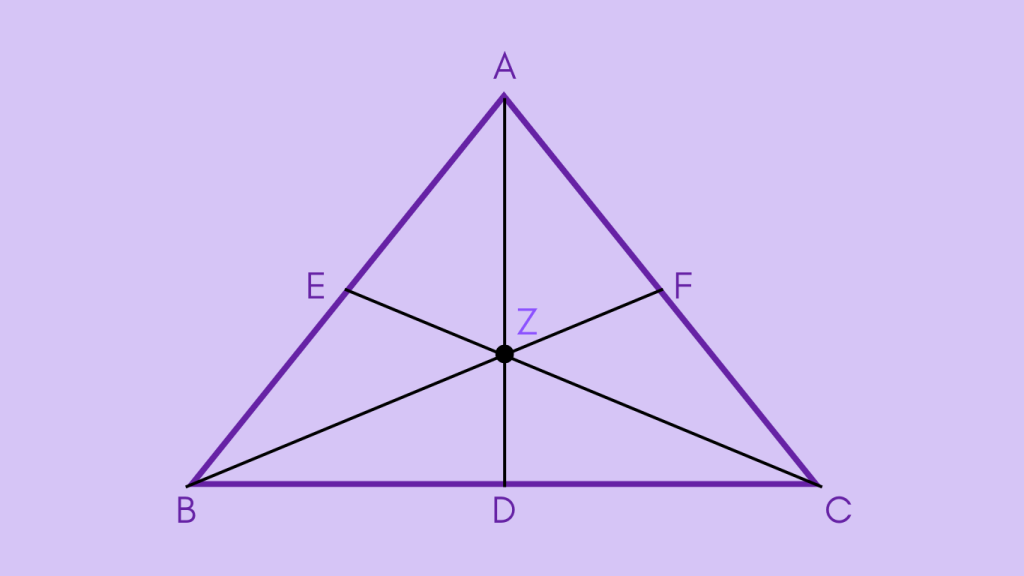
Method
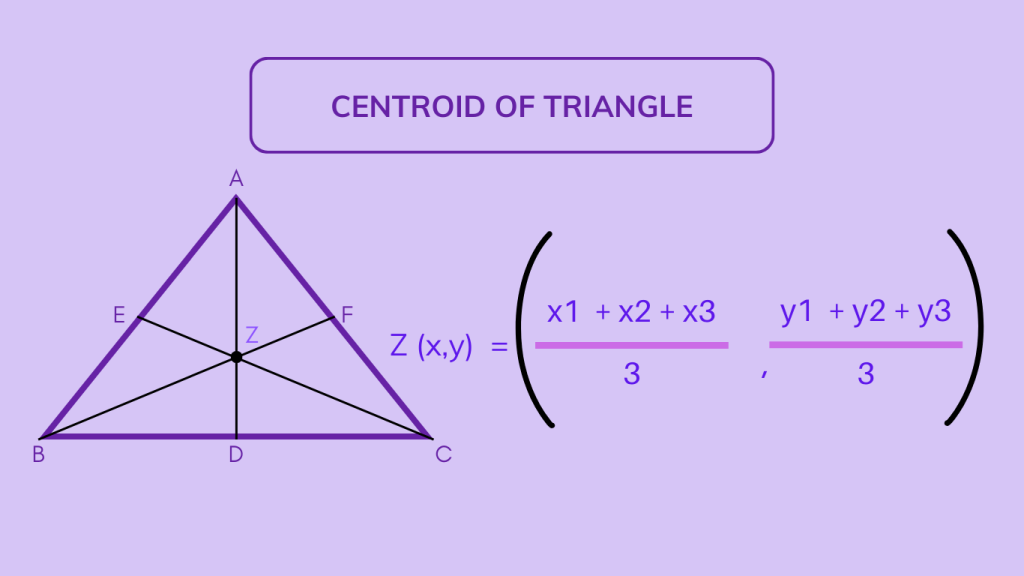
Calculating the Centroid of a Triangle
To find the coordinates of the Centroid of a Triangle, the formula (x, y) = ((x1 + x2 + x3) / 3, (y1 + y2 + y3) / 3) is utilized, where (x1, y1), (x2, y2), and (x3, y3) are the coordinates of the triangle’s vertices.
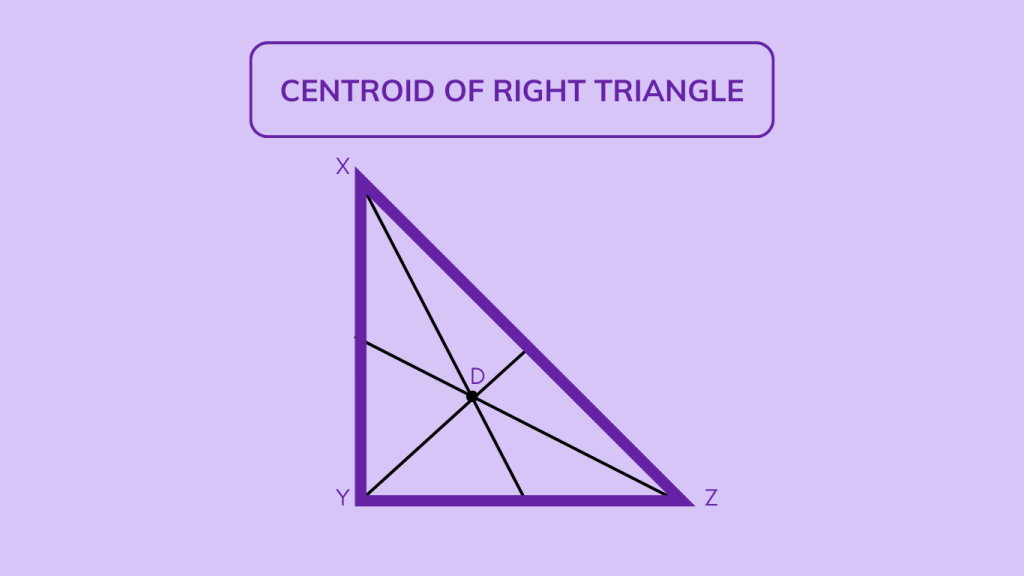
Centroid of Right Triangle
The centroid of a right triangle is the point where the three medians intersect, acting as the “center of mass” or balance point of the triangle. In a right triangle, the centroid can be found by averaging the coordinates of the three vertices, resulting in a point that is always inside the triangle. This point divides each median into two segments, with the segment closer to the vertex being twice as long as the segment closer to the midpoint of the opposite side.
Properties of Centroid of a Triangle
- Intersection Point: The centroid is the point where the three medians of the triangle intersect.
- Center of Mass: It acts as the “center of mass” or balance point of the triangle.
- Location: The centroid is always located inside the triangle.
- Median Division: It divides each median into two segments, with the segment closer to the vertex being twice as long as the segment closer to the midpoint of the opposite side.
- Coordinate Average: The centroid can be found by averaging the coordinates of the three vertices.
- Balancing Point: If the triangle were made of a uniform material, the centroid is the point at which it would balance perfectly.
Examples
Example 1: Given the vertices A(3, 4), B(7, 2), and C(5, 6) of a triangle, the coordinates of the centroid Z can be calculated using the formula.
Summary:
This example illustrates the process of finding the Centroid of a Triangle using the formula (x, y) = ((x1 + x2 + x3) / 3, (y1 + y2 + y3) / 3). By substituting the coordinates of the triangle’s vertices, the centroid is determined, providing insight into the geometric properties of the triangle.
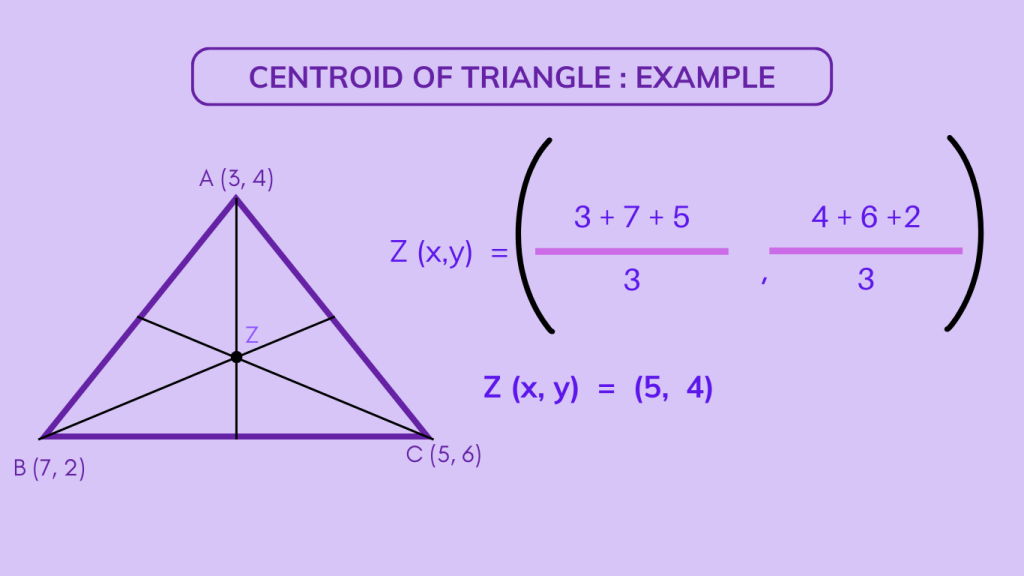
This example illustrates the process of finding the Centroid of a Triangle using the formula (x, y) = ((x1 + x2 + x3) / 3, (y1 + y2 + y3) / 3). By substituting the coordinates of the triangle’s vertices, the centroid is determined, providing insight into the geometric properties of the triangle.
Quiz
Tips and Tricks
1. Centroid of a Right Triangle
Tip: In a right triangle, the centroid is located one-third of the distance from the right angle along the hypotenuse, making it a significant point in the geometry of right triangles.
2. Properties of the Centroid
Tip: The centroid divides the medians in a 2:1 ratio and is always located inside the triangle, serving as the center of mass and being equidistant from each vertex.
3. Calculating the Coordinates
Tip: To calculate the coordinates of the centroid, use the formula (x, y) = ((x1 + x2 + x3) / 3, (y1 + y2 + y3) / 3) with the coordinates of the triangle’s vertices.
Real life application
Scenario: Architectural Design
The concept of the centroid of a triangle finds practical applications in architectural design, particularly in determining the center of mass and balance in structural elements such as trusses and load-bearing components.
FAQ's
The Centroid of a Triangle holds great importance in geometry as it represents the point of intersection of the three medians of the triangle, dividing each median into a 2:1 ratio.
The Centroid of a Triangle is defined as the point of concurrency of the three medians of the triangle, which are the line segments joining each vertex to the midpoint of the opposite side.
The formula to find the coordinates of the Centroid of a Triangle is (x, y), where x = (x1 + x2 + x3) / 3 and y = (y1 + y2 + y3) / 3, with (x1, y1), (x2, y2), and (x3, y3) being the coordinates of the triangle’s vertices.
The Centroid of a Triangle divides the medians in a 2:1 ratio, and it is always located inside the triangle. Additionally, the centroid is the center of mass of the triangle and is equidistant from each of the triangle’s vertices.
In the case of a right triangle, the centroid is located one-third of the distance from the right angle along the hypotenuse, making it a crucial point in the geometry of right triangles.
Like? Share it with your friends
Facebook
Twitter
LinkedIn