Understanding the Role of Divisor in Division
Table of Contents
Introduction
Divisors
In the realm of mathematics, the concept of division plays a crucial role in breaking down numbers into equal parts. At the heart of division lies the divisor, an essential component that determines the number of equal parts a given quantity is divided into. Let’s explore the significance of the divisor and its role in the division process.
Analogy of Definition
What are Divisors?
The divisor is a number by which another number is divided. In a division equation, the divisor is the quantity that specifies the number of equal parts the dividend is divided into. It is an integral part of the division process and is essential for determining the quotient and remainder. Understanding divisors is quite straightforward. Suppose we want to divide 42 by 6. This division is represented as 42 ÷ 6 = 7. Here, 42 is the dividend, 6 is the divisor, and 7 is the quotient.
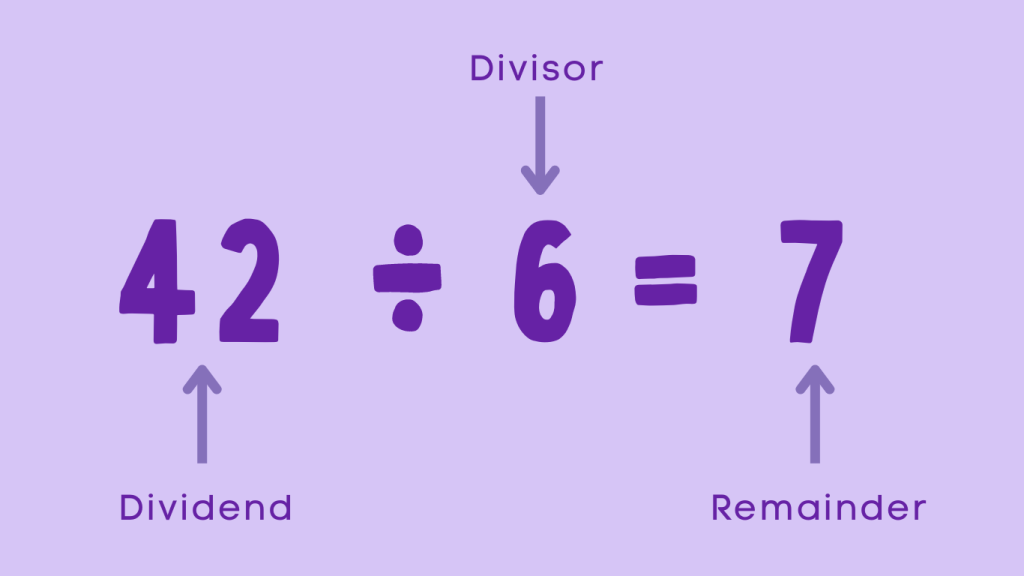
Parts of Division
In any division operation, we encounter four key components:
Dividend: This is the number or quantity that is being divided.
Divisor: The divisor is the number by which the dividend is divided.
Quotient: It is the result of the division operation, representing the number obtained by dividing the dividend by the divisor.
Remainder: This is the number that remains after the division process, which may occur when the division is not exact.
Method
Understanding Divisor
Let’s assume that we have 10 balls in total, and we need to divide them into groups of 5. In this case, 5 is the divisor because we need to divide the whole of 10 into parts of 5.
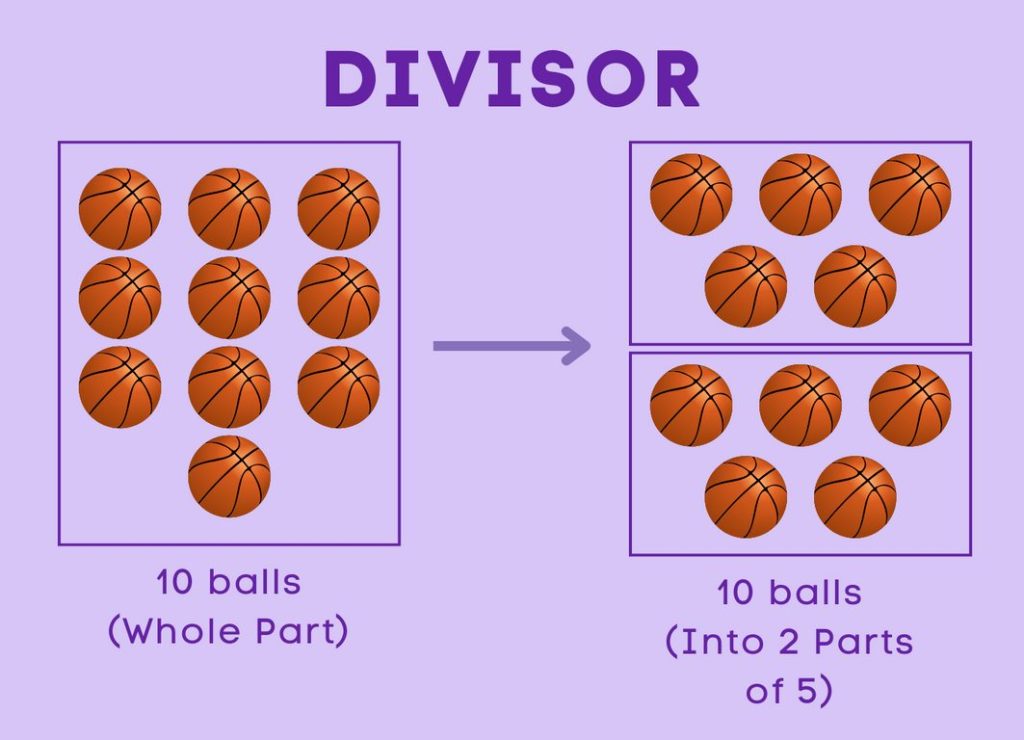
Finding the Divisor
The divisor can be found using the divisor formula, which is expressed as:
This formula helps in calculating the divisor when the dividend and quotient are known. Additionally, the divisor can be determined by identifying the factors of the dividend and understanding their relationship with the quotient.
Examples
Consider the division problem: 24 ÷ 6 = 4
In this example, 24 is the dividend, 6 is the divisor, 4 is the quotient, and 0 is the remainder. The divisor, 6, determines the number of equal parts into which 24 is divided, resulting in 4 as the quotient.
Consider the division problem: 15 ÷ 3 = 5
In this example, 15 is the dividend, 3 is the divisor, 5 is the quotient, and 0 is the remainder. The divisor, 3, determines the number of equal parts into which 15 is divided, resulting in 5 as the quotient.
Consider the division problem:36 ÷ 9 = 4
In this example, 36 is the dividend, 9 is the divisor, 4 is the quotient, and 0 is the remainder. The divisor, 9, determines the number of equal parts into which 36 is divided, resulting in 4 as the quotient.
Consider the division problem: 48 ÷ 12 = 4
In this example, 48 is the dividend, 12 is the divisor, 4 is the quotient, and 0 is the remainder. The divisor, 12, determines the number of equal parts into which 48 is divided, resulting in 4 as the quotient.
Consider the division problem: 27 ÷ 9 = 3
In this example, 27 is the dividend, 9 is the divisor, 3 is the quotient, and 0 is the remainder. The divisor, 9, determines the number of equal parts into which 27 is divided, resulting in 3 as the quotient.
Quiz
Tips and Tricks
1. Divisor in Division
Tip: The divisor is the number by which the dividend is divided to obtain the quotient and remainder in a division operation.
2. Divisor Formula
Tip: Use the formula Divisor = Dividend ÷ Quotient to calculate the divisor when the dividend and quotient are known.
3. Properties of Divisor
Tip: The divisor has the property of determining the number of equal parts the dividend is divided into, influencing the resulting quotient and remainder.
4. Divisor vs. Dividend
Tip: Distinguish between the divisor and dividend by understanding their roles in the division process. The divisor is the number being divided, while the dividend is the number by which the division is performed.
5. Parts of Division
Tip: Familiarize yourself with the three main parts of a division operation: dividend, divisor, and quotient, each playing a distinct role in the division process.
Real life application
Story: “The Divisor Chronicles”
The concept of the divisor found its way into the real world, impacting various scenarios and everyday situations.
Scenario 1: Sharing Treats
In a classroom, a teacher distributed 24 candies among 6 students. The divisor, 6, determined the number of candies each student received, resulting in an equal distribution of treats.
Scenario 2: Budget Allocation
A group of friends decided to divide their expenses equally for a trip. The total cost of the trip, the dividend, was divided by the number of friends, the divisor, to determine the individual share of each friend.
Scenario 3: Time Management
A project manager allocated tasks to team members based on the divisor of the total workload. By dividing the tasks equally, the team members were able to manage their time effectively and complete the project on schedule.
FAQ's
The divisor plays a crucial role in division by determining the number of equal parts the dividend is divided into, leading to the calculation of the quotient and remainder.
The divisor has the property of influencing the resulting quotient and remainder in a division operation. It determines the number of equal parts the dividend is divided into.
The divisor formula, Divisor = Dividend ÷ Quotient, provides a method to calculate the divisor when the dividend and quotient are known, aiding in the division process.
The main parts of a division operation are the dividend, divisor, and quotient, each playing a distinct role in the division process.
Yes, negative numbers can be divisors just like positive numbers. However, when dealing with negative divisors, it’s essential to consider the sign conventions and rules for operations involving negative numbers.
Like? Share it with your friends
Facebook
Twitter
LinkedIn