Comparing Fractions: Exploring Methods and Applications

Introduction

Comparing Fractions

In the realm of mathematics, the skill of comparing fractions plays a pivotal role in understanding their relative magnitudes and making informed decisions. Let’s delve into the methods of comparing fractions and explore their practical applications in real-life contexts.

Analogy of Definition

How to Compare Fractions?

Comparing fractions involves determining the relative sizes of two or more fractions and identifying which fraction is larger, smaller, or if they are equal in value.

Method

Methods for Comparing Fractions

There are several methods to compare fractions, including finding a common denominator, converting to decimals, and using visual representations such as fraction bars or circles.

Comparing Fractions with Like Denominator

If the denominators of the fractions are the same, or if the fractions are like fractions, then comparing them becomes simple. All we have to do to compare like fractions are to look at the numerator. The fraction with the higher number numerator will be the greater fraction. Let’s look at an example

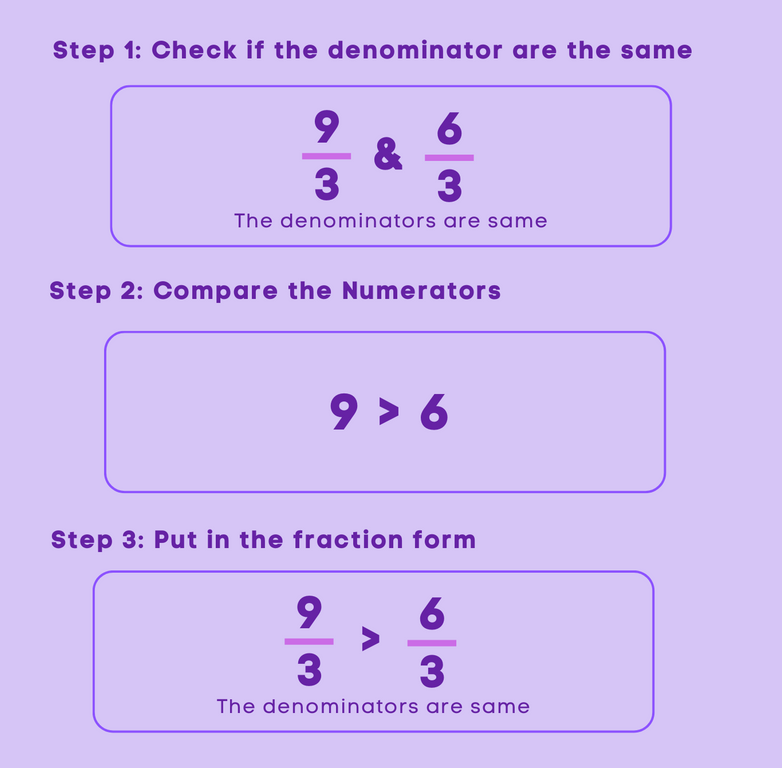
Comparing Unlike Fractions

The fractions with diferent denominators are known as unlike fractions. To compare such fractions, we will have to convert them into like fractions by finding out the LCM of the denominators. Then, we will compare the numerators like we did for like fractions.

For example: Comparing the fractions $\frac{2}{6}$ and $\frac{7}{8}$

Comparing Decimals

We can compare fractions by converting it into decimals. To convert the fractions to decimal, we need to divide the numerator by the denominator. Then, we compare the decimals.

Let’s compare $\frac{2}{6}$ and $\frac{7}{8}$

Step 1: Convert the fractions into decimals. $\frac{2}{6}$ = 0.33 and $\frac{7}{8}$ = 0.87

Step 2: Compare the decimal numbers, 0.87 > 0.33

Step 3: Since 0.87 > 0.33, $\frac{7}{8}$ > $\frac{2}{6}$

Examples

Example 1:

Scenario: Comparing 3/4 and 5/8
Method: Finding a common denominator
Calculation: 3/4 = 6/8, 5/8
Comparison: 6/8 > 5/8
Conclusion: 3/4 is greater than 5/8.

Example 2:

Scenario: Comparing 1/3 and 2/5
Method: Converting to decimals
Calculation: 1/3 ≈ 0.333, 2/5 = 0.4
Comparison: 0.333 < 0.4
Conclusion: 1/3 is less than 2/5.

Example 3:

Scenario: Comparing 2/7 and 3/9
Method: Visual representation using fraction bars
Comparison: 2/7 is visually smaller than 3/9
Conclusion: 2/7 is less than 3/9.

Summary:
These examples illustrate the methods of comparing fractions, including finding a common denominator, converting to decimals, and using visual representations. By applying these methods, the relative sizes of fractions can be determined, enabling informed comparisons and decision-making in various mathematical contexts and real-life scenarios.

Quiz

Tips and Tricks

1. Common Denominator Method

Tip: Find a common denominator for both fractions, then compare the numerators. For example, to compare $\frac{1}{3}$ and $\frac{2}{5}$ , find a common denominator (15 in this case), then compare $\frac{5}{15}$ and $\frac{6}{15}$ . Since $\frac{6}{15}$ is greater than $\frac{5}{15}$ , $\frac{2}{5}$ is greater than $\frac{1}{3}$ .

2. Cross Multiplication Method

Tip: Multiply the numerator of the first fraction by the denominator of the second fraction, and vice versa. Then compare the results. For example, to compare $\frac{1}{3}$ and $\frac{2}{5}$ , cross multiply to get 5 × 1 = 5 and 3 × 2 = 6. Since 6 is greater than 5, $\frac{2}{5}$ is greater than $\frac{1}{3}$ .

3. Visualize on a Number Line

Tip: Represent each fraction on a number line. This can help visualize which fraction is greater. For example, if you represent $\frac{1}{3}$ and $\frac{2}{5}$ on a number line from 0 to 1, you’ll see that $\frac{2}{5}$ is closer to 1 than $\frac{1}{3}$ , making it greater.

4. Convert to Decimals

Tip: Convert both fractions to decimals and then compare them. For example, $\frac{1}{3}$ ≈ 0.333 and $\frac{2}{5}$ ≈ 0.4. Since 0.4 is greater than 0.333, $\frac{2}{5}$ is greater than $\frac{1}{3}$ .

5. Benchmark Fractions

Tip: Know some benchmark fractions (like 1/2, 1/3, 1/4, etc.) and use them as references. For example, if you’re comparing $\frac{1}{3}$ and $\frac{3}{4}$ you know that $\frac{1}{3}$ is smaller than $\frac{1}{2}$ , and $\frac{3}{4}$ is greater than $\frac{1}{2}$ , so $\frac{3}{4}$ must be greater than $\frac{1}{3}$ .

Real life application

Scenario: Recipe Adjustments
When adjusting a recipe to serve a larger or smaller number of people, the skill of comparing fractions is utilized to proportionally increase or decrease ingredient quantities while maintaining the recipe’s integrity.
Scenario: Budget Planning
In budget planning, comparing fractions helps in allocating resources and expenses proportionally, ensuring that each category receives the appropriate share of the budget.
Scenario: Art and Design
In art and design, understanding and comparing fractions is essential for creating visually appealing compositions and determining proportions in various artistic elements.

FAQ's

What is the importance of comparing fractions?

Comparing fractions is essential in understanding their relative sizes and making informed decisions in various mathematical and real-life scenarios.

How can fractions be compared?

Fractions can be compared using methods such as finding a common denominator, converting to decimals, or using visual representations like fraction bars or circles.

Why is it important to find a common denominator when comparing fractions?

Finding a common denominator is crucial when comparing fractions to ensure that the fractions are expressed in the same units, allowing for accurate comparison of their sizes.

Can fractions with different denominators be compared directly?

Fractions with different denominators cannot be compared directly. They need to be converted to equivalent fractions with a common denominator before comparison.

In what real-life situations can the skill of comparing fractions be applied?

The ability to compare fractions is valuable in various real-life scenarios such as recipe adjustments, budget planning, and understanding proportions in art and design.

Like? Share it with your friends

Comparing Fractions: Exploring Methods and Applications

Table of Contents

Introduction