Understanding the Concept of Dividend in Division
Table of Contents
Introduction
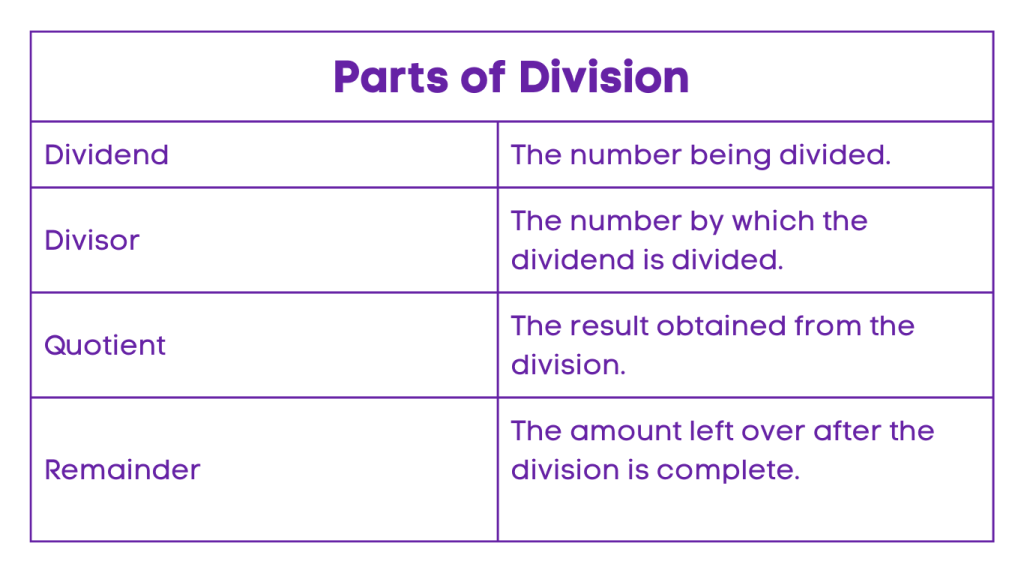
Dividend
When it comes to division, the term “dividend” plays a crucial role in the process. Understanding how to find the dividend and its relation to the divisor, quotient, and remainder is essential in mastering the concept of division.
Analogy of Definition
What is Dividend?
In division, the dividend is the number that is being divided. It is the total quantity or amount that is to be divided into equal parts. The dividend is the starting point of the division process and is divided by the divisor to obtain the quotient and remainder.
Parts of Dividend
Method
How to find the Dividend?
To find the dividend, you need to know the divisor, quotient, and remainder. The dividend can be calculated using the formula:
This formula helps in determining the original quantity or amount that was divided to obtain the given quotient and remainder.
Identifying Dividend
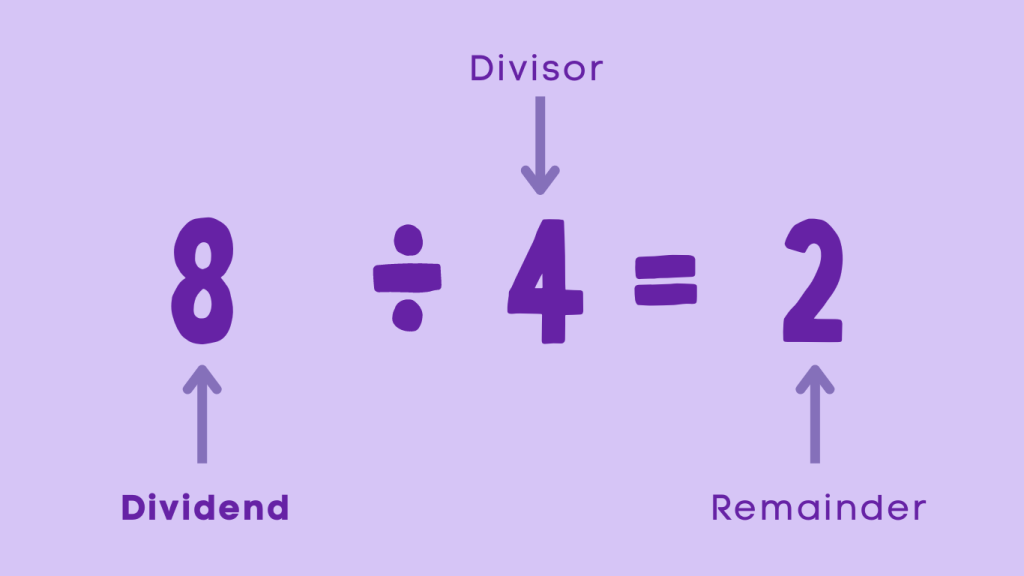
Let’s assume that we are dividing 8 by 4 . Here, since we are dividing a total number of 8, it is the dividend.
Examples
Example 1: Suppose we have a division problem where the divisor is 5, the quotient is 8, and the remainder is 3. To find the dividend, we use the formula:
Dividend = (5 * 8) + 3
Dividend = 40 + 3
Dividend = 43
So, the dividend in this example is 43.
Example 2: 24, Divisor: 6 → 24 ÷ 6 = 4
Explanation: The total number of items to be divided is 24. When we divide 24 by 6, we get 4 as the quotient. This means we can form 4 groups with 6 items each.
Example 3: 32, Divisor: 8 → 32 ÷ 8 = 4
Explanation: There are 32 objects in total. Dividing 32 by 8 gives us 4 as the result. So, we can distribute the 32 items into 8 groups, each containing 4 items.
Example 4: Dividend: 18, Divisor: 3 → 18 ÷ 3 = 6
Explanation: The total count of items is 18. When we divide 18 by 3, we obtain 6. This implies that we can create 6 groups, each with 3 items.
Quiz
Tips and Tricks
1. Understand its Role
Tip: The dividend is the total quantity or number being divided in a division operation. It’s essential to understand its significance in the division process.
2. Identify the Dividend
Tip: In a division problem, the dividend is typically the number that comes before the division symbol. For example, in “24 ÷ 6 = 4,” 24 is the dividend.
3. Check for Patterns
Tip: Look for patterns in the dividend that can make division easier. For example, if the dividend is a multiple of the divisor, the quotient will be a whole number without a remainder.
4. Estimation
Tip: When dealing with large numbers, rounding the dividend can simplify the division process. Round the dividend to the nearest multiple of the divisor for quicker mental calculations.
5. Focus on Place Value
Tip: Understanding the place value of digits in the dividend can help in long division. Start dividing from the leftmost digit and work towards the right to ensure accuracy.
Real life application
Story: “The Dividend Adventures of Emma and Noah”
Emma and Noah, two curious siblings, encountered real-life scenarios where the concept of dividend played a significant role in solving everyday problems.
Scenario 1: The Candy Store Dilemma
Emma and Noah visited a candy store with 24 candies and decided to share them equally among 6 friends. Using the formula Dividend = (Divisor * Quotient) + Remainder, they calculated the original quantity of candies, which turned out to be 24.
Scenario 2: The Pizza Party Challenge
During a pizza party, Emma and Noah had 8 slices of pizza, and after each person took 2 slices, 2 slices were left over. By applying the formula Dividend = (Divisor * Quotient) + Remainder, they determined that the original number of slices was 26.
Scenario 3: The Book Donation Drive
As part of a book donation drive, Emma and Noah distributed 45 books among 9 students. Using the formula Dividend = (Divisor * Quotient) + Remainder, they found that the original number of books was 45.
FAQ's
In division, the dividend is divided by the divisor to obtain the quotient and remainder. The relationship can be expressed as: Dividend = (Divisor * Quotient) + Remainder.
The dividend is calculated using the formula: Dividend = (Divisor * Quotient) + Remainder. This formula helps in determining the original quantity or amount that was divided to obtain the given quotient and remainder.
Yes, the dividend can be larger than the divisor in division. The dividend represents the total quantity or amount being divided, and it may or may not be evenly divisible by the divisor.
If the remainder is zero in a division problem, it indicates that the dividend is evenly divisible by the divisor, and the quotient is a whole number without any remainder.
Yes, the concept of dividend has practical applications in everyday scenarios, such as sharing items among a group, distributing resources, and calculating the original quantity of items before division.
Like? Share it with your friends
Facebook
Twitter
LinkedIn