Dividing Fractions: Methods and Step-by-Step Guide
Table of Contents
Introduction
Dividing Fractions
Dividing fractions is a fundamental operation in mathematics that allows for the precise distribution and comparison of quantities. Let’s delve into the methods and step-by-step guide for dividing fractions to gain a comprehensive understanding of this essential concept.
Method
Methods for Dividing Fractions
There are several methods for dividing fractions, including finding the reciprocal of the divisor and multiplying it by the dividend, using the ‘keep, change, flip’ approach, and converting the division into multiplication by multiplying by the reciprocal of the divisor.
Let’s try dividing \frac{3}{6} and \frac{2}{5}
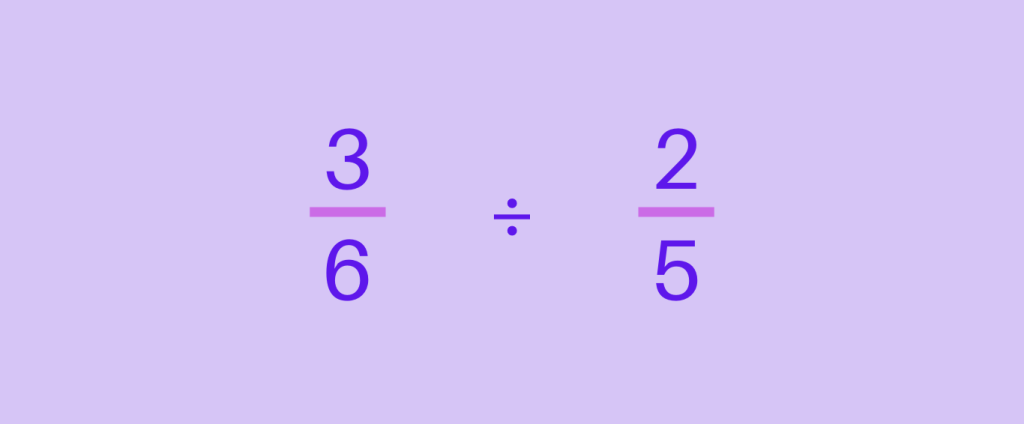
Step 1: Keep the dividend as it is
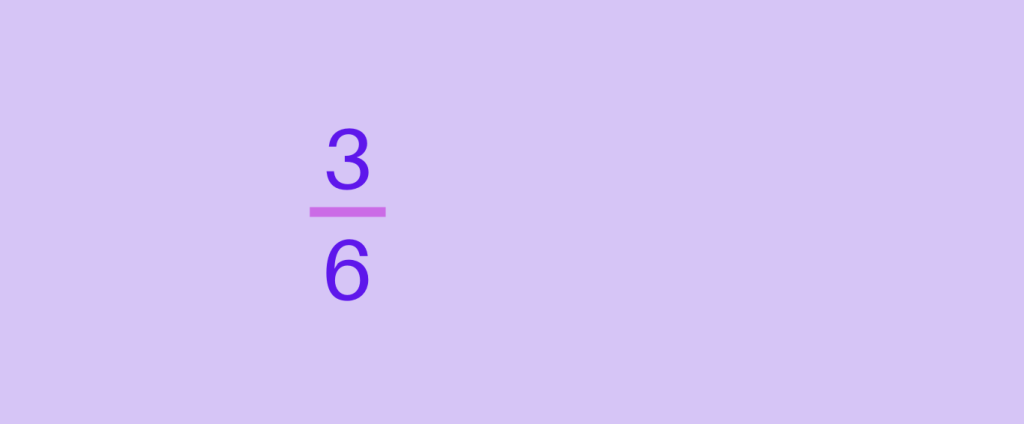
Step 2: Change the division sign into multiplication sign.
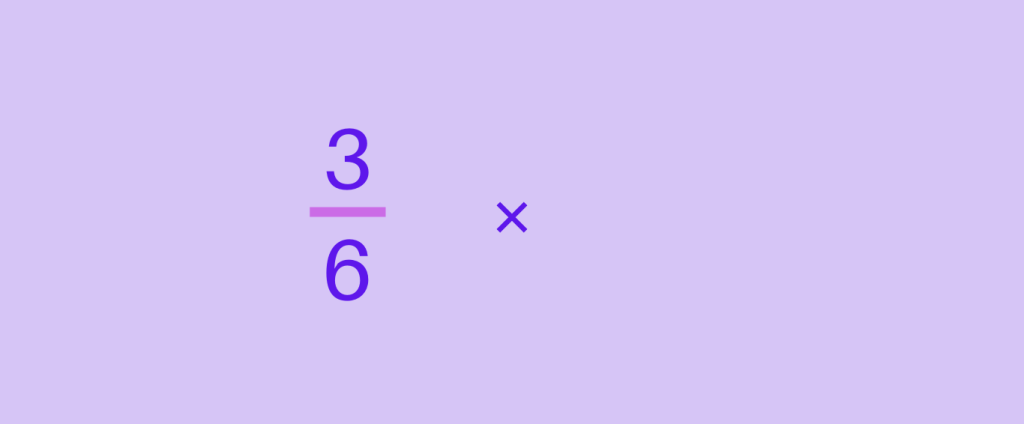
Step 3: Flip the divisor. The flipping of the divisor is also known as reciprocal.
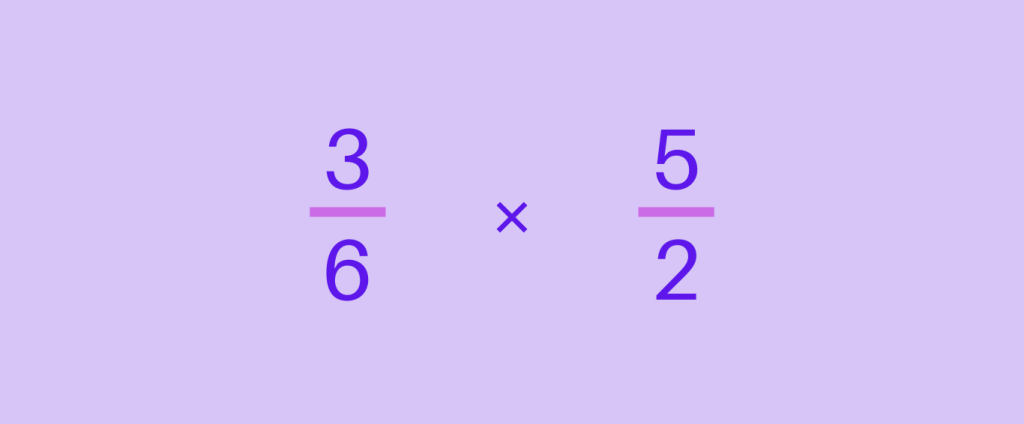
Step 4: Carry out the multiplication of the fractions.
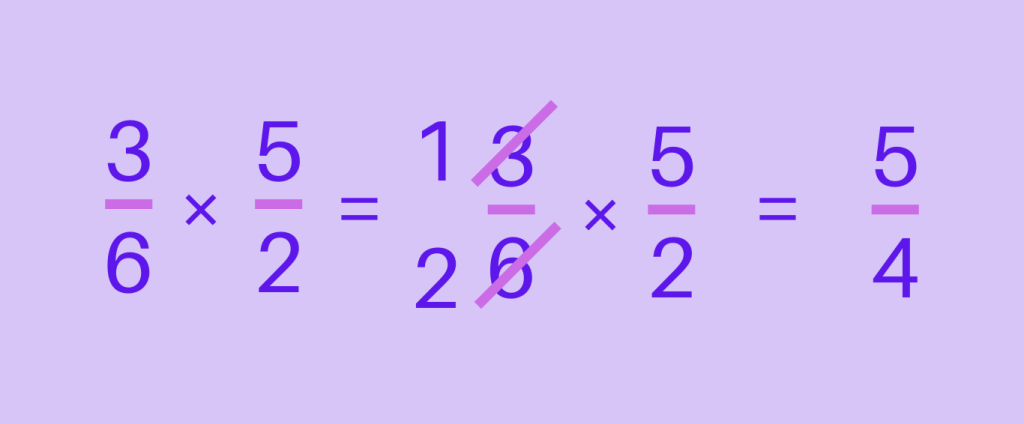
Dividing Fractions by a Whole Number
The process of dividing fraction by a whole number is similar to dividing fractions. All we have to do is put 1 as a denominator of the whole number, and carry on the division.
Let’s divide \frac{3}{5} by 9
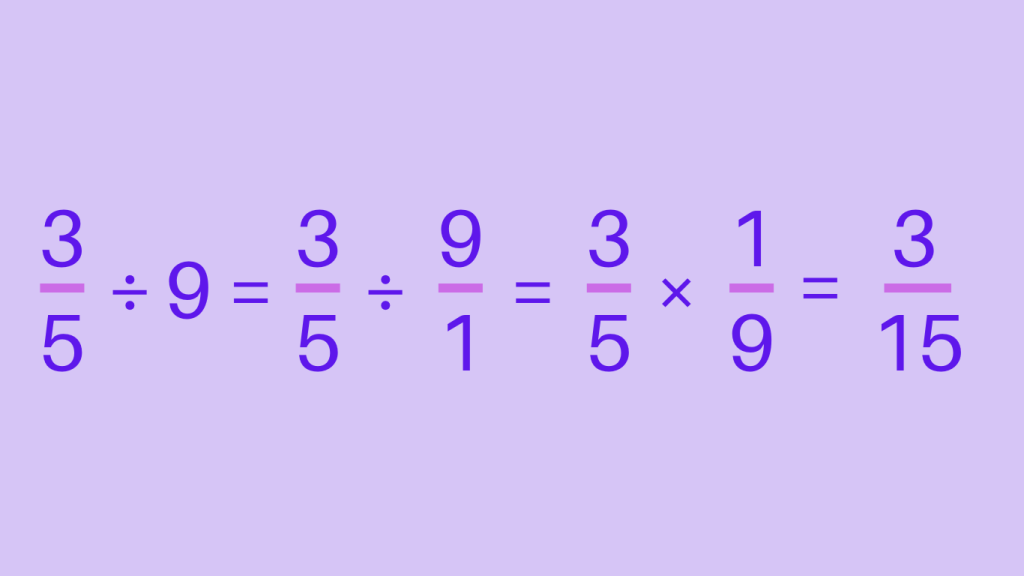
Examples
Example 1: \frac{3}{4} and \frac{1}{2}
Step 1: \frac{3}{4}  ÷ \frac{1}{2}
Step 2: \frac{3}{4} × \frac{1}{2}
Step 3: \frac{3}{4} × \frac{2}{1}
Step 4: \frac{3}{4} × \frac{2}{1} = \frac{3}{2}
Example 2: \frac{2}{3} and \frac{4}{5}
Step 1: \frac{2}{3}  ÷ \frac{4}{5}
Step 2: \frac{2}{3} × \frac{4}{5}
Step 3: \frac{2}{3} × \frac{5}{4}
Step 4: \frac{2}{3} × \frac{5}{4} = \frac{5}{6}
Summary:
These examples illustrate the step-by-step process of dividing fractions using different methods. Whether finding the reciprocal of the divisor, applying the ‘keep, change, flip’ approach, or converting the division into multiplication, the goal is to obtain the quotient of the two fractions and simplify the result if necessary.
These examples illustrate the step-by-step process of dividing fractions using different methods. Whether finding the reciprocal of the divisor, applying the ‘keep, change, flip’ approach, or converting the division into multiplication, the goal is to obtain the quotient of the two fractions and simplify the result if necessary.
Quiz
Tips and Tricks
1. Reciprocal Rule
Tip: To divide fractions, multiply the first fraction by the reciprocal of the second fraction. The reciprocal of a fraction is obtained by flipping it upside down. For example, to divide \frac{2}{3} by \frac{4}{5} , you multiply \frac{2}{3} by \frac{5}{4}.
2. Keep, Change, Flip
Tip: This is a helpful mnemonic for remembering the reciprocal rule. Keep the first fraction, change the division sign to multiplication, and flip the second fraction. For example, \frac{2}{3}  ÷ \frac{4}{5} becomes \frac{2}{3} × \frac{5}{4}
3. Cancel Common Factors
Tip: Before multiplying, cancel out any common factors between the numerators and denominators to simplify the fractions. This can make the calculation easier and reduce the size of the numbers involved.
4. Multiply Numerators and Denominators
Tip: Once you’ve canceled any common factors, multiply the numerators together to find the numerator of the result, and multiply the denominators together to find the denominator of the result.
5. Simplify the Result
Tip: After multiplying, if possible, simplify the resulting fraction by reducing it to lowest terms. T
Real life application
Real-Life Applications of Dividing Fractions:,
Scenario: Cooking and Baking
Dividing fractions is commonly used in adjusting recipes and calculating ingredient proportions in cooking and baking. Whether halving a recipe or doubling the ingredients, the concept of dividing fractions ensures accurate measurements and consistent results.
Scenario: Construction and Engineering
In construction and engineering, dividing fractions is applied to solve measurement problems, calculate proportions for materials, and determine the distribution of resources. From laying out building foundations to designing structural components, the precise division of quantities is crucial for successful projects.
FAQ's
Dividing fractions is essential in various mathematical and real-life scenarios, such as cooking, measurements, and problem-solving. It allows for the precise distribution of quantities and the comparison of different fractions.
The key concepts in dividing fractions include finding the reciprocal of the divisor, multiplying the dividend by the reciprocal of the divisor, and simplifying the resulting fraction to its lowest terms.
Yes, dividing fractions can be simplified by converting the divisor to its reciprocal and then multiplying the dividend by the reciprocal of the divisor. The resulting fraction can then be simplified to its lowest terms if necessary.
The common methods for dividing fractions include finding the reciprocal of the divisor and multiplying it by the dividend, using the ‘keep, change, flip’ approach, and converting the division into multiplication by multiplying by the reciprocal of the divisor.
The concept of dividing fractions finds practical applications in various real-life scenarios, such as adjusting recipes, calculating proportions in cooking, and solving measurement problems in construction and engineering.
Like? Share it with your friends
Facebook
Twitter
LinkedIn