Understanding Obtuse Triangles: Definition and Types
Table of Contents
Introduction
Obtuse Triangles
When exploring the realm of geometry, the concept of obtuse triangles emerges as a fundamental element. Let’s delve into the definition and types of obtuse triangles to gain a comprehensive understanding of their properties and applications.
Analogy of Definition
What are Obtuse Triangles?
An obtuse triangle is characterized by having one angle that measures more than 90 degrees, known as the obtuse angle. This type of triangle is distinct from acute and right triangles, and its properties play a significant role in geometric calculations and constructions.
Method
Types of Obtuse Triangles
There are three primary types of obtuse triangles: obtuse scalene triangle, obtuse isosceles triangle, and right obtuse triangle. Each type exhibits unique characteristics based on the relationship between side lengths and angle measurements.
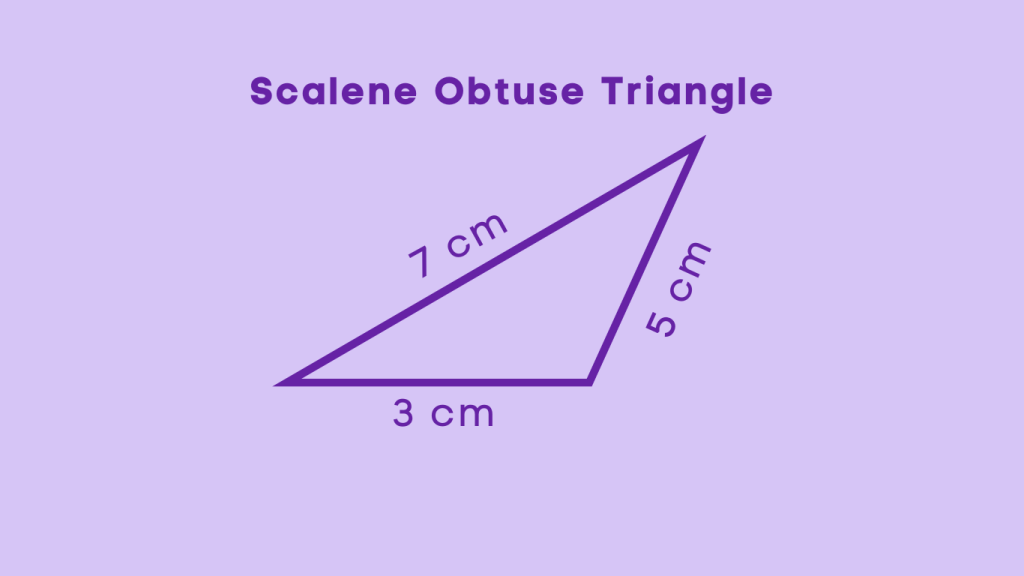
Scalene Obtuse Triangle
A scalene obtuse triangle is a triangle in which all three sides have different lengths, and one of the angles is obtuse. This means that none of the sides are equal in length, and one angle measures more than 90 degrees. Scalene obtuse triangles come in various shapes and sizes, but they all share the characteristic of having no equal sides or angles, with one angle being obtuse.
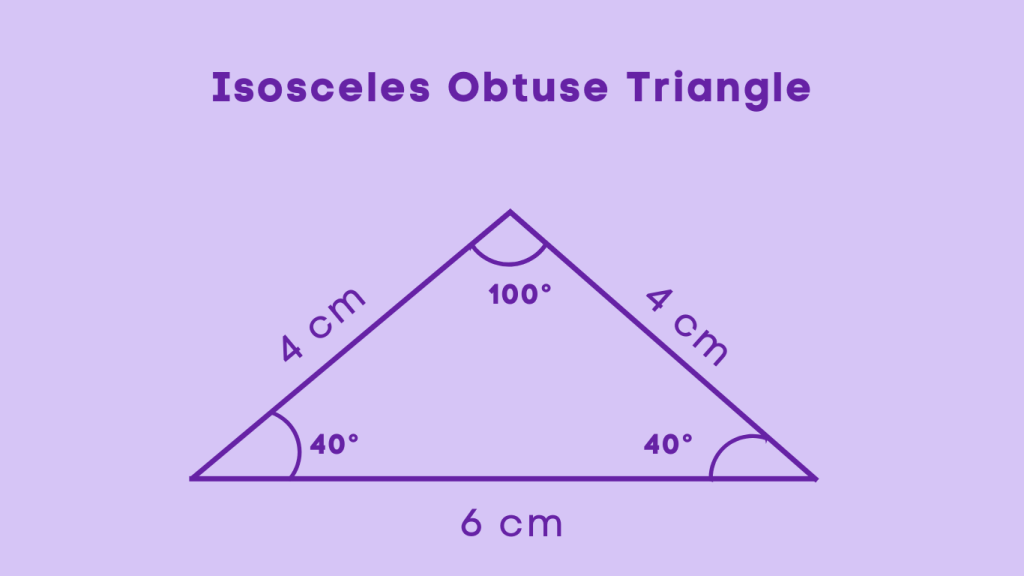
Isosceles Obtuse Triangle
An isosceles obtuse triangle is a triangle in which at least two sides have the same length, and one of the angles is obtuse. This means that two sides are equal in length, while the third side may be of a different length, and one angle measures more than 90 degrees. Despite having equal sides, isosceles obtuse triangles maintain one obtuse angle, which distinguishes them from other types of triangles.
Examples
Example 1: Obtuse Scalene Triangle
Scenario: In an obtuse scalene triangle, the side lengths are unequal, and all three angles are different. One angle measures 110 degrees, while the other two angles measure 35 degrees and 35 degrees, respectively.
Example 2: Obtuse Isosceles Triangle
Scenario: An obtuse isosceles triangle has two equal sides and two equal angles, with one angle measuring 100 degrees and the other two angles measuring 40 degrees each.
Example 3: Right Obtuse Triangle
Scenario: In a right obtuse triangle, one angle measures 90 degrees, and the other angle measures 100 degrees, while the third angle measures 70 degrees.
Summary:
These examples illustrate the distinct characteristics of obtuse triangles, including obtuse scalene triangles, obtuse isosceles triangles, and right obtuse triangles. Each type showcases the presence of an obtuse angle measuring more than 90 degrees, highlighting the unique properties of obtuse triangles in geometric contexts.
These examples illustrate the distinct characteristics of obtuse triangles, including obtuse scalene triangles, obtuse isosceles triangles, and right obtuse triangles. Each type showcases the presence of an obtuse angle measuring more than 90 degrees, highlighting the unique properties of obtuse triangles in geometric contexts.
Quiz
Tips and Tricks
1. Identifying Obtuse Triangles
Tip: Given a triangle with angle measurements, identify the type of obtuse triangle based on the angle measurements and side lengths.
2. Constructing Obtuse Triangles
Tip: To draw an obtuse triangle, start by drawing a line segment to represent one side. Then, draw two more line segments to form angles that are less than 90 degrees with the first side. Finally, extend one of the line segments beyond 90 degrees to create an obtuse angle.
3. Measuring Angles
Tip: You can estimate whether an angle is obtuse without measuring it precisely. If the angle looks wider than a right angle (90 degrees), but not as wide as a straight angle (180 degrees), then it’s likely obtuse.
4. Angle Sum Property
Tip: In any triangle, the sum of the interior angles is always 180 degrees. For an obtuse triangle, one of the angles is greater than 90 degrees. To find the measure of the third angle, subtract the measures of the two acute angles from 180 degrees.
Real life application
Scenario: Architectural Design
In architectural design, obtuse triangles are utilized in the construction of roof trusses and gable ends, where angles greater than 90 degrees are required to support the structural integrity of buildings.
Scenario: Engineering and Construction
Engineers and construction professionals use obtuse triangles in the design of bridges, support beams, and other structural elements to ensure stability and load-bearing capacity.
Scenario: Geometric Art and Design
Artists and designers incorporate obtuse triangles in geometric patterns and compositions to create visually appealing and structurally sound artworks.
FAQ's
An obtuse triangle is a type of triangle in which one of the angles measures more than 90 degrees. This angle is referred to as the obtuse angle, and it is always opposite the longest side of the triangle.
There are three main types of obtuse triangles: obtuse scalene triangle, obtuse isosceles triangle, and right obtuse triangle. An obtuse scalene triangle has three unequal sides and three different angles, with one angle measuring more than 90 degrees. An obtuse isosceles triangle has two equal sides and two equal angles, with one angle measuring more than 90 degrees. A right obtuse triangle has one angle that measures exactly 90 degrees and another angle that measures more than 90 degrees.
No, an equilateral triangle by definition has all three angles measuring 60 degrees, making it impossible for an equilateral triangle to have an obtuse angle measuring more than 90 degrees.
The sum of the angles in any triangle, including an obtuse triangle, is always 180 degrees. In an obtuse triangle, the sum of the two acute angles is less than 90 degrees, while the obtuse angle measures more than 90 degrees.
Obtuse triangles have practical applications in various fields such as architecture, engineering, and design. They are utilized in the construction of roof trusses, bridges, and other structural elements where angles greater than 90 degrees are required.
Like? Share it with your friends
Facebook
Twitter
LinkedIn