Understanding Real Numbers: Definition and Properties
Table of Contents
Introduction
Real Numbers
Real numbers form the bedrock of mathematical analysis, encompassing a wide range of numerical values that are essential in various mathematical disciplines. Let’s delve into the realm of real numbers and unravel their significance and properties.
Analogy of Definition
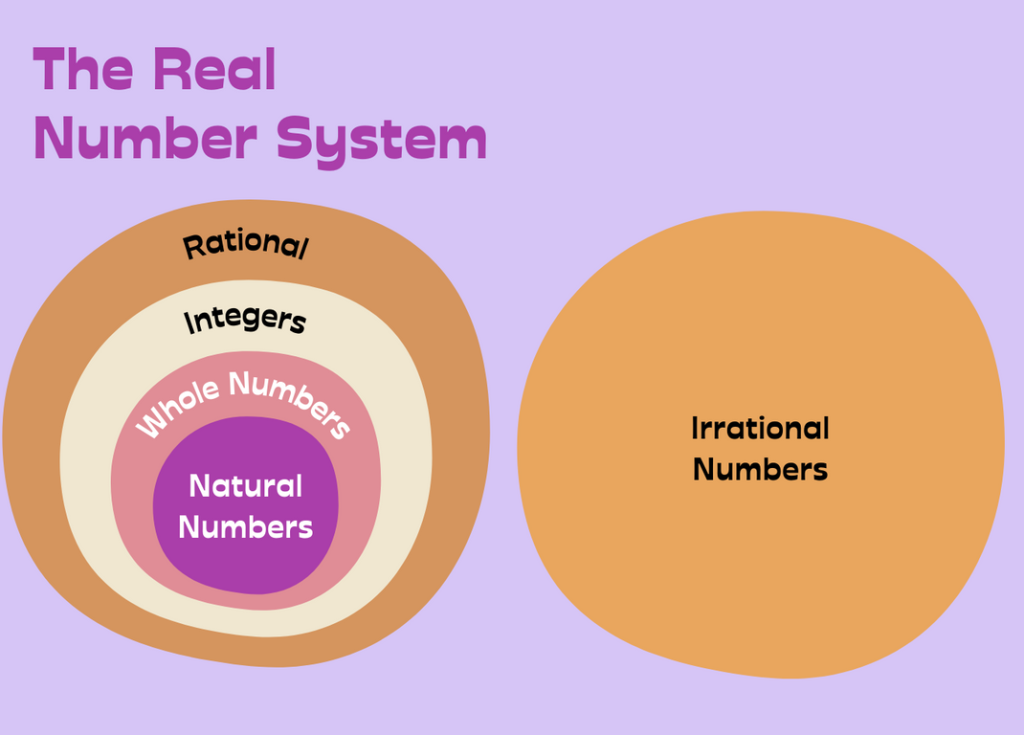
What are Real Numbers?
Real numbers encompass all rational and irrational numbers, providing a comprehensive set of values for mathematical operations and calculations. They are represented on the number line and play a fundamental role in mathematical analysis and problem-solving.
Types of Real Numbers
Real numbers are categorized into several types based on their properties and characteristics. Here’s a simple explanation of each type:
1. Natural Numbers (N): These are the counting numbers, starting from 1 and going infinitely (1, 2, 3, …). They represent the quantity of objects in the real world.
2. Whole Numbers (W): Whole numbers include all the natural numbers along with zero (0, 1, 2, 3, …). They are used for counting and measurement, including situations where zero is relevant.
3. Integers (Z): Integers are whole numbers along with their negatives and zero (… -3, -2, -1, 0, 1, 2, 3, …). They are used to represent both quantities and directions.
4. Rational Numbers (Q): Rational numbers can be expressed as fractions where the numerator and denominator are integers, and the denominator is not zero. This includes terminating decimals (decimals that end) and repeating decimals (decimals with a repeating pattern).
5. Irrational Numbers (I): Irrational numbers cannot be expressed as fractions and have decimal representations that are non-repeating and non-terminating. They include numbers like the square root of non-perfect squares (e.g., √2, √3), transcendental numbers (e.g., π, e), and many square roots of prime numbers.
Method
Properties of Real Numbers
Real numbers exhibit several key properties, including closure under addition and multiplication, the existence of additive and multiplicative identities, the commutative and associative properties, and the distributive property. These properties form the foundation for mathematical operations involving real numbers.
1. Closure Property: Real numbers are closed under addition and multiplication. This means that when you add or multiply two real numbers, the result is always a real number. For example, adding or multiplying any two real numbers will always yield another real number.
2. Commutative Property: Addition and multiplication of real numbers are commutative. This means that changing the order of the numbers being added or multiplied does not change the result. For example, a + b = b + a and a × b = b × a for any real numbers a and b.
3. Associative Property: Addition and multiplication of real numbers are associative. This means that when adding or multiplying three or more numbers, the grouping of the numbers does not affect the result. For example, (a + b) + c = a + (b + c) and (a × b) × c = a × (b × c) for any real numbers a, b, and c.
4. Distributive Property: Multiplication distributes over addition for real numbers. This means that a number multiplied by the sum of two other numbers is equal to the sum of the products of the number multiplied by each of the other two numbers individually. For example, a × (b + c) = a × b + a × c for any real numbers a, b, and c.
5. Identity Elements: The real number 0 serves as the additive identity, meaning that adding 0 to any real number leaves it unchanged (a + 0 = a for any real number a). The real number 1 serves as the multiplicative identity, meaning that multiplying any real number by 1 leaves it unchanged (a × 1 = a for any real number a).
6. Inverse Elements: Every real number has an additive inverse, which is the negative of the number. Adding a real number to its additive inverse results in 0 (a + (-a) = 0 for any real number a). Similarly, every nonzero real number has a multiplicative inverse, which is the reciprocal of the number. Multiplying a real number by its multiplicative inverse results in 1 (a × (1/a) = 1 for any nonzero real number a).
Examples
Example 1: Addition of Real Numbers
Scenario: Adding 3.5 and 2.8
Calculation: 3.5 + 2.8 = 6.3
Result: The sum of 3.5 and 2.8 is 6.3.
Example 2: Multiplication of Real Numbers
Scenario: Multiplying 4.2 and 1.5
Calculation: 4.2 × 1.5 = 6.3
Result: The product of 4.2 and 1.5 is 6.3.
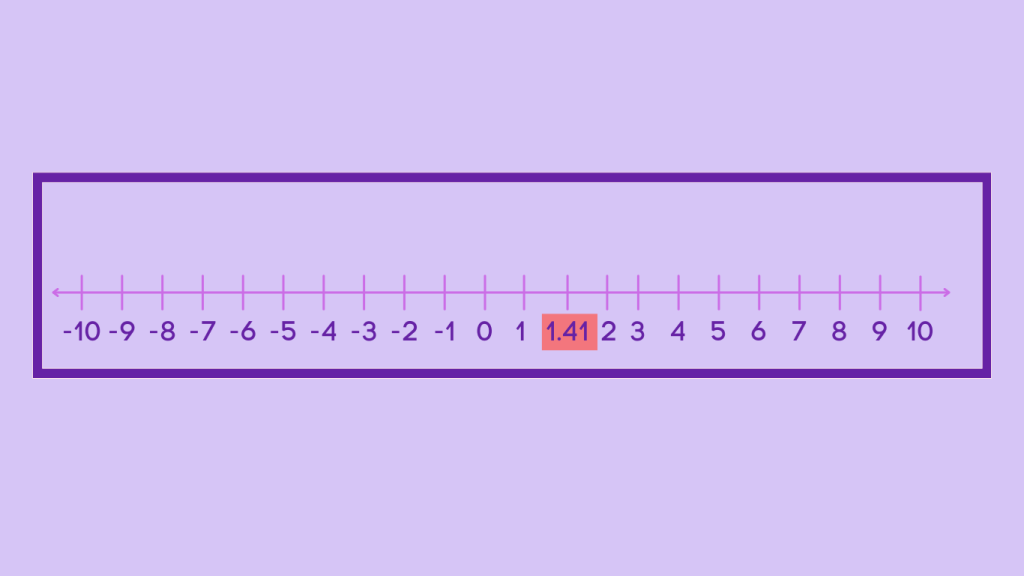
Example 3: Real Numbers on the Number Line
Scenario: Representing √2 on the number line
Calculation: √2 is approximately 1.41 and can be located between 1 and 2 on the number line.
Result: √2 lies between 1 and 2 on the number line, illustrating the presence of irrational numbers among real numbers.
Summary:
These examples demonstrate the application of real numbers in basic arithmetic operations such as addition and multiplication, as well as their representation on the number line. Real numbers encompass both rational and irrational numbers, providing a comprehensive framework for numerical analysis and calculations.
These examples demonstrate the application of real numbers in basic arithmetic operations such as addition and multiplication, as well as their representation on the number line. Real numbers encompass both rational and irrational numbers, providing a comprehensive framework for numerical analysis and calculations.
Quiz
Tips and Tricks
1. Closure Property
Tip: The sum of any two real numbers is always a real number.
2. Identity Property
Tip: The product of any real number and 1 is the original real number.
3. Commutative Property
Tip: The order of addition does not affect the sum of real numbers.
4. Associative Property
Tip: The grouping of real numbers does not affect the product.
5. Distributive Property
Tip: The distribution of a real number across addition follows a specific pattern.
Real life application
Scenario: Engineering Design
Real numbers are utilized in engineering design to perform calculations for structural analysis, material properties, and system modeling, enabling engineers to design and optimize various structures and systems.
Scenario: Financial Analysis
Real numbers play a crucial role in financial analysis, facilitating the evaluation of investment opportunities, risk assessment, and financial forecasting, providing a quantitative basis for decision-making in the realm of finance.
Scenario: Scientific Research
Real numbers are fundamental in scientific research, serving as the basis for quantitative analysis, data interpretation, and mathematical modeling in fields such as physics, chemistry, and biology, enabling the exploration of natural phenomena and scientific principles.
FAQ's
Real numbers are crucial in mathematics as they encompass all rational and irrational numbers, providing a comprehensive framework for numerical operations and calculations.
Real numbers differ from other types of numbers such as integers and fractions as they include all possible values on the number line, including both rational and irrational numbers.
Real numbers exhibit various properties such as closure under addition and multiplication, the existence of an additive identity and multiplicative identity, the commutative and associative properties, and the distributive property.
Real numbers find practical applications in fields such as science, engineering, economics, and everyday life, serving as the foundation for quantitative analysis and problem-solving.
Understanding real numbers is essential in mathematics as it forms the basis for advanced concepts such as calculus, algebra, and mathematical modeling, enabling the exploration of complex mathematical phenomena and relationships.
Like? Share it with your friends
Facebook
Twitter
LinkedIn