Understanding Acute Triangles: Types and Applications
Table of Contents
Introduction
Acute Triangles
Acute triangles are a fundamental concept in geometry, characterized by their unique angles and side lengths. Let’s delve into the world of acute triangles, exploring their types, properties, and real-life applications.
Method
Types of Acute Triangles
Acute triangles can be categorized into three main types based on their side lengths: scalene acute triangle, isosceles acute triangle, and equilateral acute triangle. Each type exhibits distinct characteristics and properties.
Scalene Acute Triangle
A scalene acute triangle is a triangle in which all three sides have different lengths, and all three angles are acute. This means that none of the sides are equal in length, and all angles measure less than 90 degrees. Scalene acute triangles come in various shapes and sizes, but they all share the characteristic of having no equal sides or angles.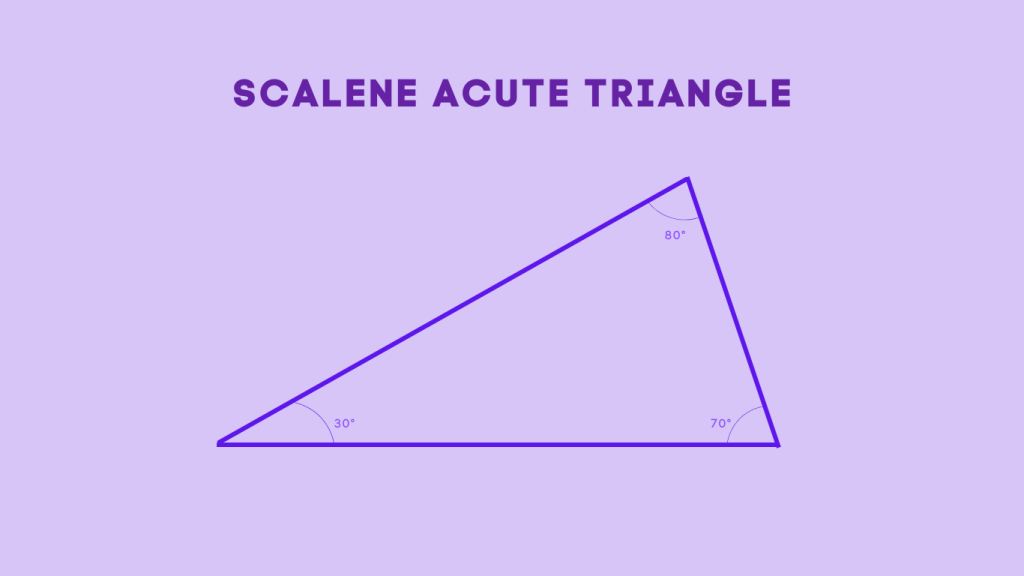
Isosceles Acute Triangle
An isosceles acute triangle is a triangle in which at least two sides have the same length, and all three angles are acute. This means that two sides are equal in length, while the third side may be of a different length. Despite having equal sides, isosceles acute triangles maintain acute angles at all three vertices. They often appear as a taller, narrower shape compared to scalene triangles.
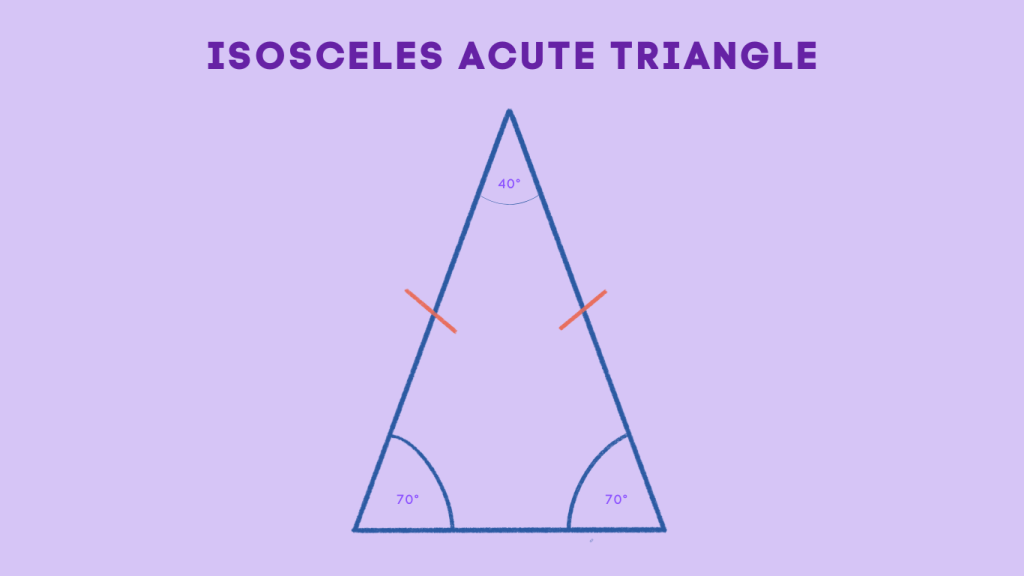
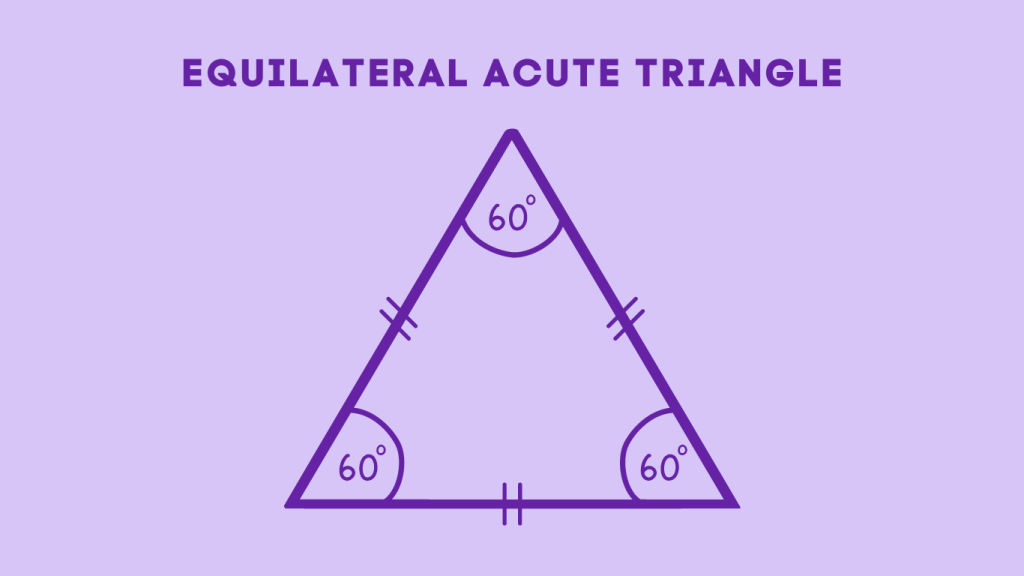
Equilateral Acute Triangle
An equilateral acute triangle is a triangle in which all three sides are of equal length, and all three angles are acute. This means that all sides are congruent, and all angles measure 60 degrees. Equilateral acute triangles have a distinctive appearance, with three equal sides and three equal angles, giving them a symmetrical and balanced shape.
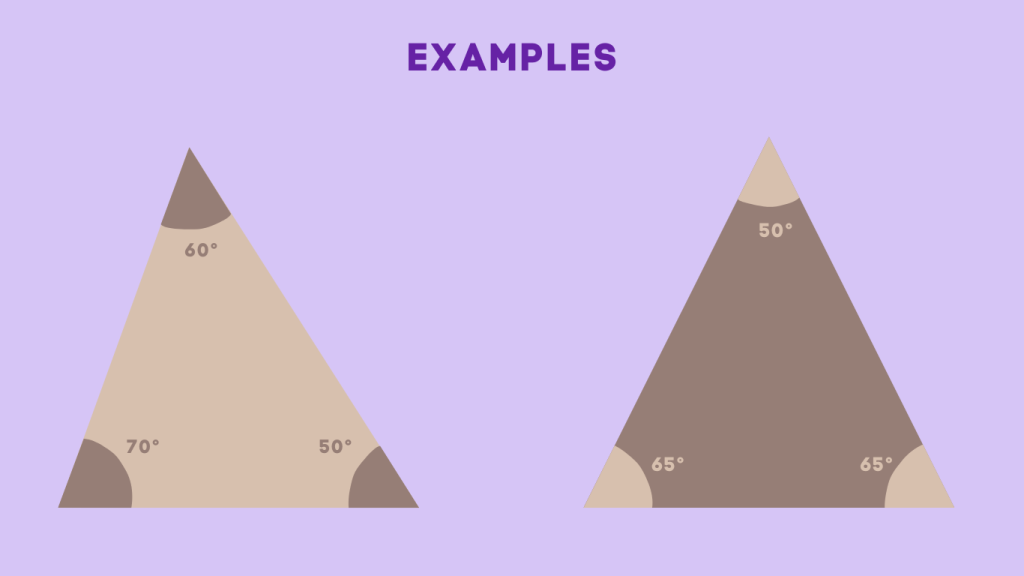
Examples
Quiz
Tips and Tricks
1. Identifying Acute Triangles
Tip: If all the angles of a triangle are less than 90°, then it is an acute triangle. For a scalene acute triangle, all sides have different lengths. For an isosceles acute triangle, two sides are of equal length. For an equilateral acute triangle, all sides are of equal length.
2. Constructing Acute Triangles
Tip: Start by drawing a line segment for the base, then use the protractor to measure and draw the acute angles. Ensure all angles are less than 90 degrees.
3. Calculating Area of Acute Triangles
Tip: To calculate the area of acute triangles, we use the formula, area = \frac{1}{2}
where,
- “base” is the length of any one side of the triangle,
- “height” is the perpendicular distance from the base to the opposite vertex.
4. Calculating Perimeter of Acute Triangles
Tip: The perimeter of an acute triangle can be calculated by adding the lengths of all three sides together. Let’s denote the lengths of the three sides as a, b, and c. Then, the perimeter (𝑃) of the triangle is given by: 𝑃 = 𝑎 + 𝑏 + 𝑐
Real life application
Scenario: Architectural Design
Acute triangles are utilized in architectural designs to create stable and aesthetically pleasing structures. The acute angles provide strength and support to the architectural elements, ensuring structural integrity.
Scenario: Engineering Blueprints
Engineers use acute triangles in blueprint designs for various structures such as bridges and buildings. The stability and balance offered by acute triangles make them essential in engineering applications.
Scenario: Navigation and Surveying
Acute triangles play a crucial role in navigation and surveying, aiding in the calculation of distances, angles, and elevation changes. Their precise angles and side lengths contribute to accurate measurements and mapping.
FAQ's
An acute triangle is a type of triangle where all three angles are less than 90 degrees, making it the opposite of an obtuse triangle.
There are three main types of acute triangles: scalene acute triangle, isosceles acute triangle, and equilateral acute triangle.
Acute triangles find applications in various fields such as architecture, engineering, and navigation due to their stability and versatility.
The properties of an acute triangle include all angles being less than 90 degrees, the sum of all angles being 180 degrees, and the sides having different lengths in the case of a scalene acute triangle.
Acute triangles can be classified as scalene acute triangles (all sides of different lengths), isosceles acute triangles (two sides of equal length), and equilateral acute triangles (all sides of equal length).
Like? Share it with your friends
Facebook
Twitter
LinkedIn
